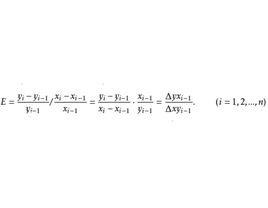彈性係數分析法

彈性係數也稱彈性，它是一個相對量，用來衡量某一變數的改變所引起的另一個變數的相對變化。彈性總是針對兩個變數而言的。例如，需求價格彈性係數所考察的兩個變數是某一特定商品的價格和需求量，而能源彈性則是考察經濟總量指標與能源消費量之間的關係。一般來說，兩個變數之間的關係越密切，相應的彈性值就越大；兩個變數越是不相關，相應的彈性值就越小。用彈性分析方法處理經濟問題的優點是簡單易行，計算方便，計算成本低，需要數據少，套用靈活廣泛。但也存在某些缺點：一是其分析帶有一定的局部性和片面性。計算彈性或作分析時，只能考慮兩個變數之間的關係，而忽略了其他相關變數所產生的影響。二是彈性分析的結果在許多情況下顯得比較粗糙，彈性係數可能隨著時間的推移而變化，以歷史數據測算出來的彈性係數預測未來，可能不準確，許多時候要分析彈性係數的變動趨勢，對彈性係數進行修正 。

定義和計算方法

彈性係數分析在經濟預測模型中是一種常用的方法，通過彈性係數的分析可以了解到，作為影響因素的自變數對某種求解的應變數的反應或影響程度。

彈性分析法又稱 彈性係數分析法，它是通過計算兩個變數的增減率的比值，考察兩個有聯繫現象間的數量關係、變化特徵和規律。 彈性係數是指因變數y的增減率與自變數x的增減率之比，常用E表示。它說明自變數x每變化百分之一，因變數y能相應地變化百分數。計算公式為：

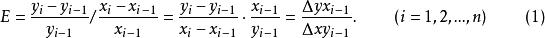彈性係數分析法

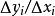彈性係數分析法

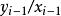彈性係數分析法

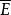彈性係數分析法

以上是逐期彈性的計算公式。本期彈性亦等於本期邊際( )乘以上期水平係數（ ）的倒數。若需計算若干期的平均彈性係數 ，有下列幾種方法可供選擇。

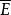彈性係數分析法

(1)水平法。用因變數和自變數的總增減率對比求 ：

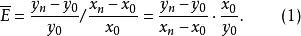彈性係數分析法

彈性係數分析法

(2)幾何法。用幾何法求得的 的平均增長率對比：

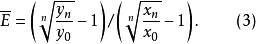彈性係數分析法

彈性係數分析法

(3)函式法。先確定 兩個變數的函式方程式，再求平均彈性；用函式法求平均彈性，通常需要與回歸分析相結合：

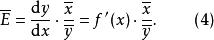彈性係數分析法

彈性的分類

彈性可按數值大小、取值正負、衡量對象不同進行分類。

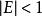彈性係數分析法

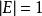彈性係數分析法

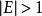彈性係數分析法

(1)按彈性係數的大小，可分為零彈性(E=0)，低彈性或弱效應彈性( )，等效應彈性( )，強效應彈性( 1)。

(2)按彈性係數取值正負，分為正效應彈性E>0和負效應彈性E<0。前者說明兩個變數之間同向變動，即正相關；後者說明兩個變數之間異向變動，即負相關。

(3)按彈性衡量對象不同，可分為需求彈性、供給彈性和產出彈性等等。其中每一類彈性又可細分為不同的彈性，如需求彈性可分為需求的收入彈性、需求的價格彈性、需求的交叉彈性或互價格彈性。產出彈性可分為產出的勞動力彈性、資本彈性和能源彈性等 。

彈性的套用

彈性在經濟社會研究和統計分析中套用較為廣泛，其主要套用有以下幾個方面 。

(1)研究現象之間的相互聯繫的數量關係。例如，運用彈性可測定居民收入變動對居民各類商品消費或需求的變動影響，研究國內生產總值變動對消費資本積累、財政收支和能源消費等變數的影響。

例1 某省城鎮居民2000~2009年人均可支配收入與人均消費支出如表1所示。這說明人均可支配收入、人均消費性支出平均每年遞增13.1%、10.6%。據此用幾何法可求得各類商品消費的平均收入彈性，其中消費的收入彈性為0. 808 6。說明收入每增長1%，消費支出可增長0.808 6%，消費的增長略慢於收入的增長，說明居民的儲蓄傾向增大。在各類商品消費的收入彈性中，食品、醫療保健、雜項商品與服務的彈性較弱，而交通通信、娛樂教育及文化服務、居住、衣著和家庭設備用品均呈現高效應彈性。這說明2000~2009年，該省城鎮居民隨著收入的增長，消費結構發生了顯著的變化，人們的溫飽問題解決後，更加注重娛樂教育及文化服務、交通通信和居住等方面的消費。

表1 2000~ 2009年某省城鎮居民消費的收入彈性係數

項 目	2000年	2009年	彈性係數E
人均可支配收入（元）	6 800. 23	20 551. 73	......
人均消費性支出（元）	5 323. 18	13 153. 00	0. 808 6
1.食品	2 189. 80	4 773. 68	0. 691 7
2．衣著	492. 10	1 297. 95	0. 870 2
3．家庭設備用品	436. 26	1 148. 85	0. 868 7
4．醫療保健	570. 37	923. 32	0. 420 5
5．交通通訊	294. 39	808. 37	0. 908 4
6．娛樂教育及文化服務	392. 38	1 721. 87	1. 365 9
7．居住	670. 56	1 968. 03	0. 971 9
8．雜項商品與服務	277. 32	510.94	0. 537 3

(2)揭示現象間數量關係的變動趨勢和規律。這種分析研究通常是把具有相互聯繫的兩個現象的時間數列聯繫起來，計算逐期彈性進行長期趨勢分析。一般來說彈性係數的變動趨勢也有遞減型、遞增型、相對穩定型和周期波動型等形態。

例2某市1993年~2004年居民人均可支配收入和住宅電話使用量如表2所示，據此計算的住宅電話使用量的收入彈性呈現遞減的趨勢，並且由正效應彈性轉為負效應彈性。這說明該市住宅電話已進入市場飽和狀態。無論居民收入怎樣增長、住宅電話需求已不再取決於收入的變化。因此，耐用品的需求收入彈性可看作是“市場飽和的預警器”

表2 某市電冰櫃需求的收入彈性

年份	電冰櫃零售量（台）	人均可支配收入（元）	彈 性
1993	2 380	1 510	......
1994	2 820	1 701	1. 461 6
1995	3 824	2 027	1. 857 7
1996	5 676	2 577	1. 784 9
1997	8 838	3 496	1. 5621
1998	11 096	4 283	1. 134 9
1999	12 326	4 838	0. 855 4
2000	13 787	5 160	0. 321 3
2001	12 998	5 425	0. 561 9
2002	12 634	6 01 3	-0. 258 4
2003	1 1 935	7 128	-0. 298 4
2004	11 624	7 527	-0. 465 5

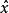彈性係數分析法

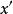彈性係數分析法

(3)用彈性係數進行預測。預測時，可先根據彈性係數的變化趨勢先確定未來時期可能達到的水平（彈性係數相對穩定時，可採用平均彈性作為預測的參數）；然後用未來時期自變數的數值或增長率，預測因變數的數值，計算公式為：

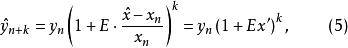彈性係數分析法

其中：n代表本期，k代表預測期。

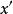彈性係數分析法

例3 某省2000年能源消費總量為1 382萬噸標準煤，國內生產總值( GDP)為898.8億元。1996~ 2000年能源消費的GDP彈性平均(E)為0.65。該省規劃2001~2005年GDP平均（）每年增長12. 5%。若能源消費彈性保持不變，要求預測能源消費總量的年平均增長率及2005年能源消費總量。

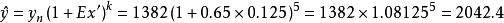彈性係數分析法

（萬噸標準煤）

預測結果表明，CDP每年遞增12.5%，則能源消費總量將每年遞增8.125%，2005年能源消費總量將達到2 042.4萬噸標準煤 。