弗雷歇-泰勒公式

弗雷歇-泰勒公式（Frechet-Taylor formula）是經典的泰勒公式在F微分意義下的推廣。

簡介

弗雷歇-泰勒公式是經典的泰勒公式在F微分意義下的推廣。

設 X 和Y是巴拿赫空間，Ω是 X 的開凸子集，x∈Ω，f:Ω→Y。若 f 在Ω上存在 n 階 F導運算元 f ，則對任意的h∈X，x+h∈Ω，成立下述泰勒公式

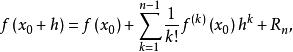弗雷歇-泰勒公式

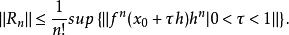弗雷歇-泰勒公式

且

推論

若f 在Ω上還是連續的，則有

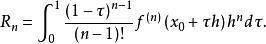弗雷歇-泰勒公式

泰勒公式

數學中，泰勒公式是一個用函式在某點的信息描述其附近取值的公式，是將一個在x=x處具有n階導數的函式f(x)利用關於(x-x)的n次多項式來逼近函式的方法。

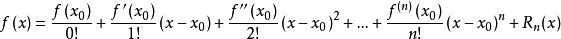弗雷歇-泰勒公式

若函式f(x)在包含x的某個閉區間[a,b]上具有n階導數，且在開區間(a,b)上具有n+1階導數，則對閉區間[a,b]上任意一點x，成立下式：其中，f(x)表示f(x)的n階導數，等號後的多項式稱為函式f(x)在x處的泰勒展開式，剩餘的R(x)是泰勒公式的餘項，是(x-x) 的高階無窮小。