簡介
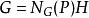弗拉蒂尼引理在有限群論， 弗拉蒂尼引理指：若有限群G有正規子群H，H有西羅子群P，則 ，其中 是P的正規化子。
它以Giovanni Frattini命名。他以此引理證明一個與弗拉蒂尼子群有關的定理。
證明
弗拉蒂尼引理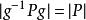
弗拉蒂尼引理
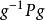弗拉蒂尼引理
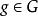弗拉蒂尼引理
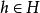弗拉蒂尼引理
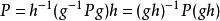弗拉蒂尼引理
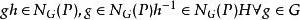弗拉蒂尼引理因為 ， ，所以可以根據西羅定理，在H內， 與P共軛 ，故對於任意的 ，存在 使得 ，因此 。
套用
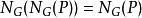弗拉蒂尼引理它套用於證明以下陳述：所有有限冪零群都是的西羅子群的直積。若P是西羅子群、G是有限群， 。
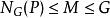弗拉蒂尼引理
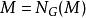弗拉蒂尼引理更一般的結果：若P是西羅子群、G是有限群，且 ，則 。
有限群
在數學裡， 有限群是有著有限多個元素的群。有限群理論中的某些部分在20世紀有著很深的研究，尤其是在局部分析和可解群與冪零群的理論中。期望有個完整的理論是太過火了：其複雜性會隨著群變得越大時而變得壓倒性地巨大。
較少壓倒性地，但仍然很有趣的是在有限域上的一些較小一般線性群。群論學家J. L. Alperin曾寫過：“有限群的典型例子為GL(n,q)－在q個元素的域上的n維一般線性群。學生在學此領域時，若以其他的例子來做介紹，則可能會被完全地誤導。（Bulletin (New Series) of the American Mathematical Society, 10 (1984) 121）此類型最小的群GL(2,3)的討論，見Visualizing GL(2,p)。
有限群和對稱有直接地關接，當其被限制在有限個轉變時。 其證明為， 連續對稱，如李群中的，也會導致有限群，如外爾群。在此一方面，有限群和其性質將能夠用在如理論物理問題的重要地方，即使其用途在一開始並不顯著。
每一素數階的有限群都是循環群。
