廣義最小二乘估計

用疊代的鬆弛算法對線性最小二乘估計的一種改進。 廣義最小二乘估計就是使估計準則J為極小的參數估計。 Design

廣義最小二乘估計

正文

用疊代的鬆弛算法對線性最小二乘估計的一種改進。線性最小二乘估計在模型誤差為相關噪聲時是有偏估計，即其估計值存在偏差。這時採用廣義最小二乘估計能獲得較精確的結果。
假設所討論的單輸入單輸出系統的差分方程模型是

式中{uk}和{yk}分別是輸入和輸出序列：

和

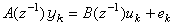
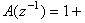
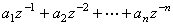
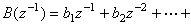
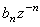
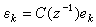是運算元多項式,它們的係數是需要通過估計來求出的未知數;z-1是單位延遲運算元；{ek}是誤差序列，它是零均值平穩相關噪聲序列。為了進行廣義最小二乘估計可以從形式上把ek變換成，這裡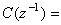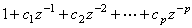，它的係數也是未知的。如果{ek}具有有理譜密度,則可把{εk}當作白噪聲序列來處理。這樣就把系統模型變成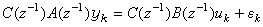

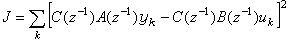
相應的估計準則是

廣義最小二乘估計就是使估計準則J為極小的參數估計。多項式A(z-1)、B(z-1)和C(z-1)的係數都是未知的,所以不能用一個線性算法獲得廣義最小二乘估計。
廣義最小二乘估計採用疊代的鬆弛算法：先行固定C(z-1)，估計A(z-1)和B(z-1),使J 趨於極小；然後固定A(z-1)和B(z-1),估計C(z-1),使 J 趨於極小。如此反覆疊代，直至估計值收斂。這時每步只進行簡單的線性最小二乘估計運算，疊代的初值取扗(z-1)=1。
廣義最小二乘估計算法的估計精度高，已得到套用並獲得不少成果。它的缺點在於：當信噪比較小時,J可能有多個局部極小點，估計結果不能保證收斂到全局最小點，即參數真值；它的計算量也比線性最小二乘估計增加很多。
這種算法也可推廣到多輸入多輸出系統，並且有相應的近似遞推估計算法。當誤差{ek}為正態噪聲序列時，這種算法還可以解釋為極大似然估計的鬆弛算法。
參考書目
　G.G.哥德溫、R.L.潘恩著，張永光、袁震東譯：《動態系統辨識：試驗設計與數據分析》，科學出版社，北京，1983。(G.C.Goodwin and R.L.Payne，dynamic system　Identification：Experiment Design and Data Analysis, Academic Press, New York,1977.)

配圖

相關連線