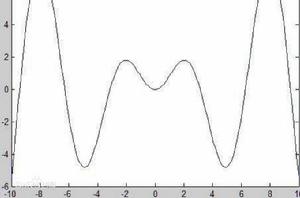
歷史上比較著名的康托(Cantor)定理,大致有下列三個:
康托定理1:閉區間上的連續實函式是一致連續的。
康托定理2:一個集合本身的勢嚴格小於其冪集的勢。
康托定理3:如果一個全序集是可列集,且是稠密的,無最大和最小值的,則它一定和有理數集序同構。
定理
 康托定理
康托定理 康托定理
康托定理 康托定理
康托定理若函式在閉區間上連續,則它在上一致連續。
 康托定理
康托定理 康托定理
康托定理 康托定理
康托定理 康托定理
康托定理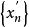 康托定理
康托定理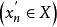 康托定理
康托定理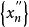 康托定理
康托定理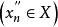 康托定理
康托定理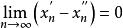 康托定理
康托定理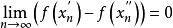 康托定理
康托定理設函式在區間上定義,則在上一致連續的充分必要條件是:對任何點列和,只要滿足,就成立。
 康托定理
康托定理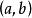 康托定理
康托定理 康托定理
康托定理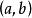 康托定理
康托定理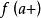 康托定理
康托定理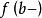 康托定理
康托定理函式在有限開區間連續,則在上一致連續的充分必要條件是與存在。
證明
採用反證法。
 康托定理
康托定理 康托定理
康托定理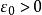 康托定理
康托定理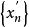 康托定理
康托定理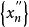 康托定理
康托定理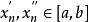 康托定理
康托定理假設在上非一致連續,由非一致連續定義可知存在及兩點列和,,滿足
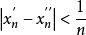 康托定理
康托定理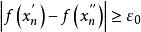 康托定理
康托定理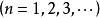 康托定理
康托定理,且。
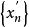 康托定理
康托定理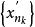 康托定理
康托定理因為有界,由Bolzano-Weierstrass定理,存在收斂子列:
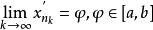 康托定理
康托定理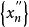 康托定理
康托定理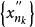 康托定理
康托定理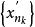 康托定理
康托定理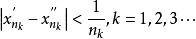 康托定理
康托定理在點列中取子列,其下標與下標相同,則由,又得到
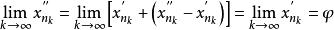 康托定理
康托定理 康托定理
康托定理 康托定理
康托定理由於函式在點連續,因而有
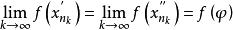 康托定理
康托定理於是得到:
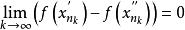 康托定理
康托定理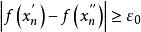 康托定理
康托定理 康托定理
康托定理 康托定理
康托定理但這與假設產生矛盾,從而推翻假設,得到在上的一致連續的結論。
開區間上連續但非一致連續的例子
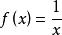 康托定理
康托定理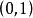 康托定理
康托定理例:在上連續,但非一致連續。
 康托定理
康托定理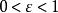 康托定理
康托定理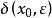 康托定理
康托定理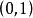 康托定理
康托定理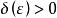 康托定理
康托定理證:對於任意給定的,,我們通過精確地解出,來說明不存在適用於整個區間的。
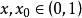 康托定理
康托定理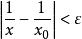 康托定理
康托定理對任意,關係式 即為
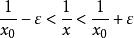 康托定理
康托定理它等價於
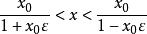 康托定理
康托定理即
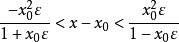 康托定理
康托定理由此得到
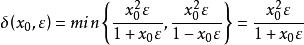 康托定理
康托定理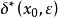 康托定理
康托定理顯然,這就是。
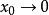 康托定理
康托定理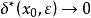 康托定理
康托定理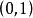 康托定理
康托定理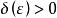 康托定理
康托定理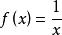 康托定理
康托定理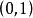 康托定理
康托定理但是當時,,換言之,不存在對區間中一切點都適用的,因此在上非一致連續。