簡介
庫爾卡尼－野水積是命名自拉溫德拉·什里帕德·庫爾卡尼和野水克己。
若h和k是對稱(0,2)-張量，定義其積為
庫爾卡尼-野水積其中Xj是切向量。
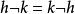庫爾卡尼-野水積從上可見 。
兩個對稱張量的庫爾卡尼－野水積，有黎曼張量的代數對稱性。因此，庫爾卡尼－野水積常用以表示里奇曲率張量和外爾張量在黎曼流形的曲率中的構成部分。這是在微分幾何中有用的里奇分解。
一個黎曼流形有常截面曲率k，若且唯若黎曼張量有以下形式
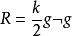庫爾卡尼-野水積其中g是度量張量。
黎曼流形
黎曼流形是一個微分流形，其中每點p的切空間都定義了點積，而且其數值隨p平滑地改變。它容許我們定義弧線長度、角度、面積、體積、曲率、函式梯度及向量域的散度。
每個R的平滑子流形可以導出黎曼度量：把R的點積都限制於切空間內。實際上，根據納什嵌入定理，所有黎曼流形都可以這樣產生。
我們可以定義黎曼流形為和R的平滑子流形是等距同構的度量空間，等距是指其內蘊度量（intrinsic metric）和上述從R導出的度量是相同的。這對建立黎曼幾何是很有用的。
黎曼流形可以定義為平滑流形，其中給出了一個切叢的正定二次形的光滑截面。它可產生度量空間：
如果γ: [a,b] →M是黎曼流形M中一段連續可微分的弧線，我們可以定義它的長度L（γ）為
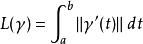庫爾卡尼-野水積（注意：γ'（t）是切空間M在γ（t）點的元素；||·||是切空間的內積所得出的範數。）
使用這個長度的定義，每個連通的黎曼流形M很自然的成為一個度量空間（甚至是長度度量空間）：在x與y兩點之間的距離d（x,y）定義為：
d(x,y) =inf{ L(γ): γ是連線x和y的一條光滑曲線}。
雖然黎曼流形通常是彎曲的，“直線”的概念依然存在：那就是測地線。
在黎曼流形中，測地線完備的概念，和拓撲完備及度量完備是等價的：每個完備性都可以推出其他的完備性，這就是Hopf-Rinow定理的內容。
