基本介紹
度量可遞性質(保測變換或平穩序列的)(metrically transitive property (of measure-preserving transformation or stationary sequence))是一種與遍歷性有密切關係的性質，人們稱保測變換T具有度量可遞性質(或者稱T是度量可遞的)，如果關於它的每一不變集有機率0或1，這又等價於每一幾乎處處不變集有機率0或1。可以證明，若變換T是度量可遞的，ξ是任一隨機變數，則有
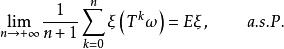度量可遞性質（保測變換或平穩序列的）
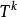度量可遞性質（保測變換或平穩序列的）
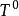度量可遞性質（保測變換或平穩序列的）即具有度量可遞性質的變換T是遍歷的，上式中的 是T的k次冪(即連續作k次T變換)， 是恆等變換。
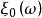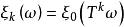度量可遞性質（保測變換或平穩序列的）
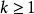度量可遞性質（保測變換或平穩序列的）
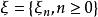度量可遞性質（保測變換或平穩序列的）
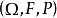度量可遞性質（保測變換或平穩序列的）
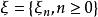度量可遞性質（保測變換或平穩序列的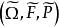） 度量可遞性質（保測變換或平穩序列的）
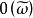度量可遞性質（保測變換或平穩序列的）
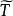度量可遞性質（保測變換或平穩序列的）
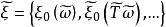度量可遞性質（保測變換或平穩序列的）
度量可遞性質（保測變換或平穩序列的）
度量可遞性質（保測變換或平穩序列的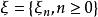） 度量可遞性質（保測變換或平穩序列的）
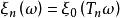度量可遞性質（保測變換或平穩序列的）
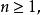度量可遞性質（保測變換或平穩序列的）設T是一保測變換， 是一隨機變數。令 對 ，則序列 是一嚴平穩序列。反之，對於 上每一嚴平穩序列 ，恆能構造定義在某一機率空間 上的隨機變數 和保測變換 ，使得 和 有相同的機率分布。因此，不失一般性，對於任意嚴平穩序列 ，可以假設存在保測變換T，使得 對所有 於是人們稱嚴平穩序列ξ具有度量可遞性質(或者稱ξ是度量可遞的)，如果上述相應於ξ的保測變換T具有同樣的性質，度量可遞的嚴平穩過程具有均值遍歷性 ：
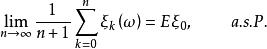度量可遞性質（保測變換或平穩序列的）相關定理
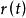度量可遞性質（保測變換或平穩序列的）定理1具有連續相關函式 的平穩正態過程為度量可遞的充要條件是此過程的增函式為連續。
定理2平穩過程為度量可遞的充要條件是： 此過程為部分混合的。
