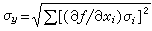度規

度規，是給定時空中兩個相鄰事件間的時空線元，又稱度量。有長度定義的空間叫度量空間，度量空間中坐標差為dxμ的兩點間的距離。

度規

正文

給定時空中兩個相鄰事件間的時空線元，又稱度量。有長度定義的空間叫度量空間,度量空間中坐標差為dxμ的兩點間的距離（線元）ds用下式表示：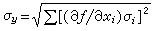

式中gμv 叫度規（係數），它是一個張量，故又叫度規張量。給定度規張量，空間的度量性質就完全確定了。例如，三維歐氏空間用直角坐標表示時，兩點間距離的平方為：

ds2=(dx1)2+(dx2)2+(dx3)2，

其度規張量為：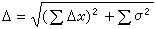

而用球坐標表示時為：

ds2=(dr)2+r2(dθ)2+r2sin2θ(d嗞)2，

其度規張量為：

有時又把用度規張量具體表示的 ds2的表達式稱為度規，例如四維閔可夫斯基時空任兩點間的線元平方值為：

ds2=(dx1)2+(dx2)2+(dx3)2－(dx4)2，

式中dx4＝cdt,ds2表示式稱為閔可夫斯基度規。度規張量為：

配圖

相關連線