定義
平面上與某一投影面成最大傾角的直線,稱為平面上對該投影面的 最大傾斜線,在平面上對某一投影面的最大傾斜線有無數條,它們是平面上的一組互相平行的直線。
平面上對某一投影面的最大傾斜線,是與平面上的該投影面的平行線相垂直的直線;它與該投影面的傾角,也就是平面對該投影面的傾角。
相關性質分析
 平面上最大傾斜線
平面上最大傾斜線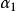 平面上最大傾斜線
平面上最大傾斜線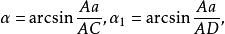 平面上最大傾斜線
平面上最大傾斜線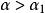 平面上最大傾斜線
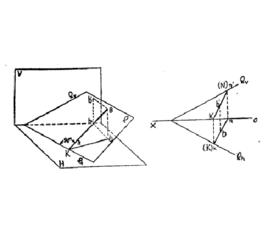
平面上最大傾斜線如圖1所示,在平面P上有一條水平線AB,過端點A在平面P上作AB的垂線AC,在平面P的水平跡線P上與H面交得點C,AC與P也交成直角。過點A作垂直於H面的投射線,與H面交得a,C點在H面上,其水平投影c就在原處,連a與c,ac就是AC的水平投影,AC與ac的夾角,即為AC對H面的傾角。在P上任取一點D,點D的水平投影d也在D的原處,將A與D、a與d相連,則ad是平面P上直線AD的水平投影,AD與ad的夾角,也是AD對H面的傾角。從圖中可見:由於在直角三角形ACD中,AD是斜邊,所以AD>AC,於是就推導出。由此就證明了平面P上只有與水平線相垂直的直線,與H面的傾角最大,也就是平面P上的對H面的 最大傾斜線。從而讀者可以聯想到:斜屋面上的雨水就是按斜屋面上的對H面的最大傾斜線的方向流下的;在斜面上如有一小球自由滾落時,滾落路線也就是過小球與斜面的接觸點在斜面上所作的對H面的最大傾斜線。
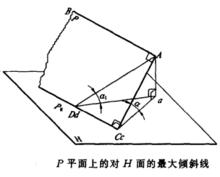 圖1
圖1 平面上最大傾斜線
平面上最大傾斜線 平面上最大傾斜線
平面上最大傾斜線 平面上最大傾斜線
平面上最大傾斜線 平面上最大傾斜線
平面上最大傾斜線由於平面P上的對H面的最大傾斜線AC⊥P,按一邊平行於投影面的直角的投影特性,ac也垂直P,由此可知平面AaC既垂直於平面P,又垂直於H面,而AC、ac分別是平面AaC與P面、H面的交線,AC和ac所夾的平面角,就是平面P與H面的兩面角,也就是平面P與H面的傾角,而AC和ac的夾角是平面P上的一條對H面的最大傾斜線與H面的傾角。由此也證明了平面上的對H面的最大傾斜線與H面的傾角,就是這個平面對H面的傾角。
 平面上最大傾斜線
平面上最大傾斜線 平面上最大傾斜線
平面上最大傾斜線 平面上最大傾斜線
平面上最大傾斜線 平面上最大傾斜線
平面上最大傾斜線同理可證:平面上與正平線相垂直的直線,是平面上的對V面的最大傾斜線,它與V面的傾角,就是該平面與V面的傾角;平面上與側平線相垂直的直線,是平面上的對W面的最大傾斜線,它與W面的傾角,就是該平面與W面的傾角。
於是就推導了上述平面上的最大傾斜線的投影特性。
例題解析
例題1 如圖2(a)所示,已知△ABC,求作△ABC平面與H面的傾角α和與V面的傾角β。
解: 根據平面上對投影面的最大傾斜線的投影特性,在△ABC平面上分別作水平線和正平線;然後,再在△ABC平面上作它們的垂線,即為△ABC平面上對H面和V面的最大傾斜線;最後,作出對H面的最大傾斜線與H面的傾角和對V面的最大傾斜線與V面的傾角,就是△ABC平面與H面的傾角α和與V面的傾角β。
求△ABC平面與H面的傾角α的作圖過程如圖2b所示:
①過a'作OX軸的平行線,與b'c'交得d’;由d‘引投影連線,與bc交得d,連a與d。ad、a'd‘即為△ABC平面上的水平線AD的兩面投影。
②過b作ad的垂線,與ad交得e;由e引投影連線,與a'd'交得e',連b'與e‘。be、b'e'就是△ABC平面上對H面的最大傾斜線BE的兩面投影。
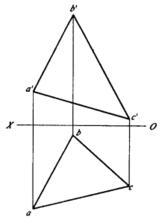 圖2(a)
圖2(a)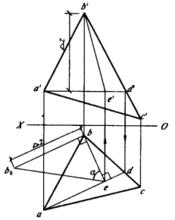 圖2(b)
圖2(b)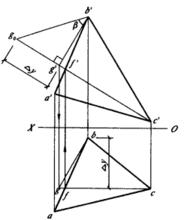 圖2(c)
圖2(c)③過b作be的垂線,在其上從b量取反映在V面投影中的點B與E的z坐標差∆z,得b;連b與e在直角三角形ebb中,be與be的夾角,即為BE與H面的傾角,也就是所求的△ABC平面與H面的傾角α。
求△ABC平面與V面的傾角β的作圖過程如圖2c所示:
①過c作OX軸的平行線,與ab交得f;由f引投影連線,與a’b’交得f’,連c'與f’。cf、c'f'’即為△ABC平面上的正平線CF的兩面投影。
②過b’作c' f’的垂線,與c’f'的延長線交得g';由g’引投影連線,與cf的延長線交得g,連b與gbg、b'g’就是△ABC平面上對V面的最大傾斜線BG的兩面投影。
③過g’作b' g’的垂線,即c'g'的延長線,在其上從g’量取反映在H面投影中的點G與B的y坐標差∆y,得g;連b’與g。在直角三角形b’g’g中,b'g與b'g’的夾角,即為BG與V面的傾角,也就是所求的△ABC平面與V面的傾角β。