簡介
帽子矩陣(hat matrix)是指一類正交投影矩陣。對帽子矩陣又叫帽變換又叫K-T變換。對於線性模型Y=Xβ+e，E(e)=0，cov(e)=σ2I，矩陣H≙...X（XTX）-1XT是將觀測向量Y正交投影到由X的列向量所生成的子空間上的投影矩陣。Y^=HY.習慣上稱H為帽子矩陣 。
帽子矩陣的性質
帽子矩陣的性質如下圖所示 ：
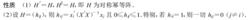帽子矩陣的性質帽子矩陣的作用
帽子矩陣在回歸診斷，殘差分析中有著特殊的作用，討論帽子矩陣H=(hij)元素性質非常重要 。
矩陣
在數學中，矩陣（Matrix）是一個按照長方陣列排列的複數或實數集合，最早來自於方程組的係數及常數所構成的方陣。這一概念由19世紀英國數學家凱利首先提出。
矩陣是高等代數學中的常見工具，也常見於統計分析等套用數學學科中。在物理學中，矩陣於電路學、力學、光學和量子物理中都有套用；計算機科學中，三維動畫製作也需要用到矩陣。 矩陣的運算是數值分析領域的重要問題。將矩陣分解為簡單矩陣的組合可以在理論和實際套用上簡化矩陣的運算。對一些套用廣泛而形式特殊的矩陣，例如稀疏矩陣和準對角矩陣，有特定的快速運算算法。關於矩陣相關理論的發展和套用，請參考矩陣理論。在天體物理、量子力學等領域，也會出現無窮維的矩陣，是矩陣的一種推廣 。
矩陣的歷史
矩陣的研究歷史悠久，拉丁方陣和幻方在史前年代已有人研究。
在數學中，矩陣（Matrix）是一個按照長方陣列排列的複數或實數集合，最早來自於方程組的係數及常數所構成的方陣。這一概念由19世紀英國數學家凱利首先提出。作為解決線性方程的工具，矩陣也有不短的歷史。成書最遲在東漢前期的《九章算術》中，用分離係數法表示線性方程組，得到了其增廣矩陣。在消元過程中，使用的把某行乘以某一非零實數、從某行中減去另一行等運算技巧，相當於矩陣的初等變換。但那時並沒有現今理解的矩陣概念，雖然它與現有的矩陣形式上相同，但在當時只是作 為線性方程組的標準表示與處理方式。
矩陣正式作為數學中的研究對象出現，則是在行列式的研究發展起來後。邏輯上，矩陣的概念先於行列式，但在實際的歷史上則恰好相反。日本數學家關孝和（1683年）與微積分的發現者之一戈特弗里德·威廉·萊布尼茨（1693年）近乎同時地獨立建立了行列式論。其後行列式作為解線性方程組的工具逐步發展。1750年，加布里爾·克拉默發現了克萊姆法則 。
