在數學領域,希爾伯特空間是歐幾里德空間的一個推廣,其不再局限於有限維的情形。與歐幾里德空間相仿,希爾伯特空間也是一個內積空間,其上有距離和角的概念(及由此引伸而來的正交性與垂直性的概念)。此外,希爾伯特空間還是一個完備的空間,其上所有的柯西列等價於收斂列,從而微積分中的大部分概念都可以無障礙地推廣到希爾伯特空間中。希爾伯特空間為基於任意正交繫上的多項式表示的傅立葉級數和傅立葉變換提供了一種有效的表述方式,而這也是泛函分析的核心概念之一。希爾伯特空間是公式化數學和量子力學的關鍵性概念之一。
描述
同一個態可以在不同的表象中用波函式來描述,所取的表象不同,波函式的形式也不同,但他們描寫同一個態。這和幾何中一個矢量可以在不同的坐標系中描寫類似。矢量A可以在直角笛卡爾坐標中用三個分量(Ax,Ay,Az)來描寫,也可以在球極坐標中用三個分量(Ar,Aθ,Aφ)來描寫等等。在量子力學中,我們可以把狀態Ψ看成是一個矢量——態矢量。選取一個特定的Q表象,就相當選取一個特定的坐標系。Q的本徵函式u1(x)u2(x)u3(x)···un(x)···是這個表象的基矢。這相當於直角坐標系中單位矢量i,j,k。波函式((a1(t)a2(t)···)是態矢量Ψ在Q表象中沿各基矢方向的“分量”。正如A沿i,j,k三個方向的分量是(AxAyAz)一樣。i,j,k是三個相互獨立的方向,說明A所在的空間是普通三維空間。量子力學中Q的本徵函式u1(x)u2(x)u3(x)···un(x)···有無限多,所以態矢量所在的空間是無限維的函式空間。這種空間在數學中稱為Hilbert空間。
優勢
與經典力學不同,量子力學中用波函式來描述微觀粒子的運動。所以在量子力學中也用不同於經典力學的方法來表示力學量,即用算符來表示微觀粒子的力學量。而量子力學中算符有其自己的性質:算符都是線性算符,算符有厄米性。所以量子力學中也稱算符為厄米算符,且厄米算符的本徵函式構成了正交、歸一、完備系。[3]在量子力學中,算符可以用矩陣表示,公式可以用矩陣表述。矩陣本身可以看成是一個級數組成的空間。而且一個粒子的態是又很多個態疊加而成的。量子力學的態空間是一個完備的線性內積空間。在量子力學的研究中,常常要得到一個本徵函式的本徵值,且本徵函式往往都是一個偏微分方程。在解偏微分時,需要解本徵值方程,常用的方法是級數法。這時需要有一個函式空間,其軸是一組正交完備系。由一組正交完備的基底通過線性疊加組成方程的解。本徵解既是在一個具體表象(固定坐標軸)中只有一個軸表示。這個空間叫做希爾伯特空間。量子力學之所以選擇Hilbert空間作為描述微觀系統狀態的函式空間,是由態函式的性質決定的,量子力學使用的數學工具主要是泛函分析。[4]所以在量子力學中引入Hilbert空間是非常必要的。
套用
在量子力學中
從數學的角度來看,量子力學是研究如何從一個線性空間得到的問題,即線性空間函式,其數學方法是以泛函分析為主。我們把空間之間的映射稱為運算元,所謂泛函不過是值域落在實直線R上或複平面C內的一個運算元,量子力學中考慮的是線性泛函書是一個定義域落在矢量空間X中,而值域落在X的標量域K中的線性運算元。在量子力學中,每個力學變數對應於一個希爾伯特算符。所要計算的力學量通過對應的希爾伯特算符,將其態函式構成的希爾伯特空間,映射到實數域而得到的。與量子力學對應的希爾伯特空間是平方可積函式的空間。
在環境科學中
在環境綜合評價中,是以每種污染物相互獨立,互不相關的假設為前提的。這在數學上就成為兩兩正交。用數學術語可以寫作
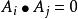 希耳伯空間
希耳伯空間這樣,我們把每一種污染物記作一個分矢量,那么N種污染物就構成了一個N維空間。這就把希耳伯空間理論引入了環境科學。其實,希耳伯空間理論在物理學、量子化學中早已獲得了廣泛的套用。如此,由N種污染物造成的環境污染就構成了在希耳伯空間中的“污染場”。而每組特定數值的N種污染物造成的環境污染狀態就可以看作是希耳伯空間中的一個向量A,而我們所要求的環境污染評價的綜合指數就是向量A的“模”值,可用下式表示:
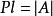 希耳伯空間
希耳伯空間對於N維(N>3)空間確是一個非常抽象的純數學概念,沒有一個客觀的實體可以與它相對應。但是三維空間是大家所熟悉的。其實,三維空間僅是任意維向量空間的一個特例。換而言之,任意維向量空間是三維空間的推廣。
在顏色測量中
目前顏色測量主要有兩種方法:一種是分光測色法,另一種是光電積分測色法。光電積分測色操作簡單、測量快捷、成本低、體積小,在生產實踐中有廣泛的套用。光電積分測色儀的主要弱點是顏色三刺激值的測量不夠準確,所以長期以來僅被當作色差計使用。測量誤差主要是由於儀器的光電系統不嚴格滿足盧瑟條件(Luther condition)所致。利用希耳伯空間向量間的投影可有效的擬合出光譜三刺激值,只要適當的選擇光電器件光譜的位置和個數,就可對光譜三刺激值準確的逼近。

