簡介
希爾伯特-施密特定理是對稱核線性積分運算元的基本定理。
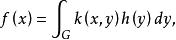希爾伯特-施密特定理
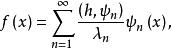希爾伯特-施密特定理
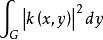希爾伯特-施密特定理設K是對稱核線性積分運算元，其核k(x,y)是平方可積的，並且不恆等於零。設{λ}和{ψ}是K的全系特徵值與全系就範正交特徵函式。設h(x)是平方可積的，令則f(x)可以表示為{ψ}的幾乎絕對一致收斂的傅立葉級數並且若有界，則上述收斂是絕對一致收斂。
套用
希爾伯特-施密特定理是希爾伯特(Hilbert,D.)和施密特(Schmidt,E.)所建立的。這一定理在對稱核線性積分方程理論中起重要作用。
有時，人們還把關於對稱核線性積分運算元的一整套理論也統稱為希爾伯特-施密特理論。
對稱核線性積分運算元
(linear integral operator with symmetric kernel)
對稱核線性積分運算元是具有對稱核的線性積分運算元，又稱為具有埃爾米特核的線性積分運算元。對稱核線性積分運算元理論，是有限維空間對稱矩陣理論在無窮維空間的推廣。
1904年，希爾伯特(D.Hilbert)從有限維空間對稱矩陣理論出發，通過取極限的方法，最早進行了對對稱核線性積分運算元的研究，施密特(E.Schmidt)等也做出了重要貢獻。對稱核線性積分運算元的理論在近代已經被抽象和推廣為希爾伯特空間上的自共軛運算元的譜分解理論。
