基本介紹
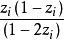 布魯爾方法
布魯爾方法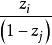 布魯爾方法
布魯爾方法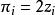 布魯爾方法
布魯爾方法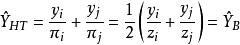 布魯爾方法
布魯爾方法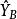 布魯爾方法
布魯爾方法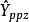 布魯爾方法
布魯爾方法布魯爾方法的具體做法是第一個單位按與 成比例的機率抽出,第二個單位按機率 抽出,其中j指抽出的第一個單位,抽樣方法中一直令 。該方法採用霍維茨-湯普森估計量: 來估計總體總值Y。該方法有兩個合乎需要的性質:一是在放回抽樣中, 的方差總是小於估計量 的方差,該結論布魯爾1963年已證明。二是不等機率不放回抽樣的方差由耶茨和格倫迪給出為:
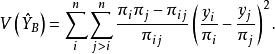 布魯爾方法
布魯爾方法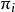 布魯爾方法
布魯爾方法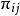 布魯爾方法
布魯爾方法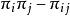 布魯爾方法
布魯爾方法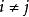 布魯爾方法
布魯爾方法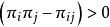 布魯爾方法
布魯爾方法式中: 指第i個單位被抽選到樣本的機率, 指第i個和第j個單位都被抽選到樣本中的機率。因 項常常變化很大,有時是負數。因此不太穩定,故爾用布魯爾方法。對於所有的 , ,故方差的估計量總是正數,該結論拉奧1965年給出代數證明。
具體說明
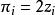 布魯爾方法
布魯爾方法當n=2時,這個抽樣方法一直使 ,並採用霍維茨-湯普森估計量
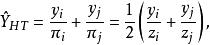 布魯爾方法
布魯爾方法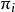 布魯爾方法
布魯爾方法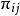 布魯爾方法
布魯爾方法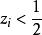 布魯爾方法
布魯爾方法採用不同的方法時,布魯爾(1963年),拉奧(1965年)和德賓(1967年)提出的方法,全都得出相同的 和 值。我們假定每個 。
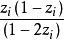 布魯爾方法
布魯爾方法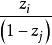 布魯爾方法
布魯爾方法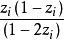 布魯爾方法
布魯爾方法布魯爾按與 成比例的他所稱的修訂過的機率抽出第一個單位,按機率 抽出第二個單位(這裡j是抽出的第一個單位)。把 轉換為實際的機率所需要的除數是它們的總和
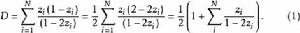 布魯爾方法
布魯爾方法當n=2時,第i個單位被抽中的機率是它在第一次被抽中的機率和第二次被抽中的機率之和。因此
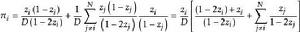 布魯爾方法
布魯爾方法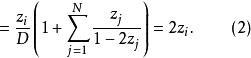 布魯爾方法
布魯爾方法這裡用到了(1)計算D的公式。與此類似,
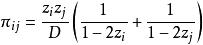 布魯爾方法
布魯爾方法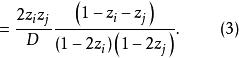 布魯爾方法
布魯爾方法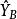 布魯爾方法
布魯爾方法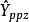 布魯爾方法
布魯爾方法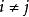 布魯爾方法
布魯爾方法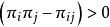 布魯爾方法
布魯爾方法這個方法有兩個合乎需要的性質:布魯爾(1963年)曾經證明,在放回抽樣中, 的方差總是小於估計量 的方差,第二,代數證明(拉奧,1965年),對於所有的 , ,因此,方差的耶茨-格倫迪估計量v總是正數。
德賓(1967年)的方法是按機率z來抽出第一個單位(i)。如果單位i在第一次被抽中,則單位j在第二次被抽中的慨率是使它與
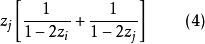 布魯爾方法
布魯爾方法成比例。
在這一情況下,比例的除數是
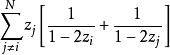 布魯爾方法
布魯爾方法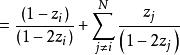 布魯爾方法
布魯爾方法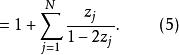 布魯爾方法
布魯爾方法因此,除數等於布魯爾方法中的2D(見(1))。所以,第i個單位在第一次被抽中,第j個單位在第二次被抽中的機率是
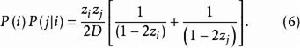 布魯爾方法
布魯爾方法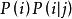 布魯爾方法
布魯爾方法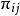 布魯爾方法
布魯爾方法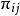 布魯爾方法
布魯爾方法由於對稱性,這等於 ,因此德賓的 與(3)中布魯爾的 是相同的。
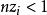 布魯爾方法
布魯爾方法桑普福德(Sampford)(1967年)曾把這個方法推廣套用到含量為n的樣本中(條件是:對總體中的所有單位 )。採用他的抽樣方法時,抽到例如由單位1,2,..., n所組成的樣本的機率是(3)的自然推廣,它與
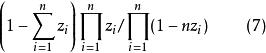 布魯爾方法
布魯爾方法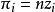 布魯爾方法
布魯爾方法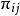 布魯爾方法
布魯爾方法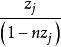 布魯爾方法
布魯爾方法對於這個方法。可以證明 。計算 的公式已經給出,並建議用電子計算機來計算它。由於採用了Y的HT估計量(霍維茨-湯普森估計量),因此可以用公式計算它的方差和估計方差,耶茨-格倫迪估計量v總是正數。桑普福德曾建議採用好幾個方法來實際抽取樣本,以滿足(7)的要求,其中的一個方法是採用放回抽樣的方式,按機率來抽取第一個單位, 按與 成比例的機率來抽取所有其餘的單位。如果得到—個包含n個不同單位的樣本,這個樣本就被接受。如果一個單位在樣本中出現了兩次,這個樣本就被拒絕接受。可以看到,這個方法導出(7)。為了得到一個樣本,需要試驗多少次,是有一個公式用來計算它的期望次數的,這可以作為這一方法的速度的指南。
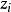 布魯爾方法
布魯爾方法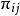 布魯爾方法
布魯爾方法當n=2時,德賓(1967年)抽取樣本的方法與布魯爾的方法不同。它有一個特點,就是在第一次抽取和第二次抽取時,抽中單位i的無條件機率都是 。在此之前,費里吉(Fellegi)(1963年)曾指出,在定期反覆進行的調查中採用多組抽樣時,由於對同一些人長期不斷地進行調查不受歡迎,因此有必要或最好是採用一種所謂定期輪換的方式,不時把一些單位拋棄而用別的單位代替它們。他創造出—個抽選連續單位的方法,它也有德賓方法的性質。他的方法以重複計算(iterative calculations)為基礎,與布魯爾-德賓的方法相似,但 稍稍不同。

