基本介紹
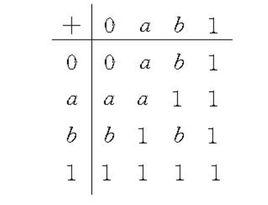
布爾加法指布爾代數B=〈B,+,·,′,0,1〉中記為+的二元運算,對任意給定的兩個元素a,b∈B,經加法運算後得到一個確定的元素c∈B,記為c=a+b,c稱為a,b的布爾和。在元素不多的情形下,常可用列表法確定布爾加法,下面是含且僅含4個元素的布爾代數的加法表,表中最左一列表示加法的第一個元素,最上一行表示加法的第二個元素,各對應行列交叉處記的是兩者的布爾和,特別,對二元布爾代數,其布爾加法若且唯若兩個元素a,b∈B都是0時,a+b才是0,否則a+b是1 。
 圖1
圖1布爾加法的運算律
下面的運算律也稱為布爾代數的運算律。
布爾代數的運算律是布爾代數的基本運算法則,布爾代數〈B,+,·,′,0,1〉有如下運算律,對B中任意元素a,b,c,有 :
1.結合律:(a+b)+c=a+(b+c) ,
(a·b)·c=a·(b·c).
2.交換律:a+b=b+a, a·b=b·a.
3.分配律:a·(b+c)=(a·b)+(a·c),
a+(b·c)=(a+b)·(a+c).
4.吸收律:a+a·b=a, a·(a+b)=a.
5.冪等律:a+a=a, a·a=a.
6.德·摩根律(反演律):(a+b)′=a′·b′,
(a·b)′=a′+b′.
7.對合律(雙重否定律):(a′)′=a.
8.互補律:a+a′=1, a·a′=0.
9.零一律(麼元律):a+0=a, a·1=a.
10.囿元律(極元律):a+1=1, a·0=0.
布爾加法和與門電路
或門執行布爾加法,其運算符為“+”。這與常規的十進制加法運算不同,在布爾加法中,1+1等於1。表1給出了2輸入或門的真值表。
| A | B | X |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
兩個變數的布爾加法(Boolean addition,即ORing)記為A+B,稱之為和項。三個變數的布爾加法可以表示為A+B+C,這與常規代數的變數加法的表示相同 。
或門的布爾表達式
(1)2輸入或門運算的布爾代數表達式為:
 布爾加法
布爾加法該布爾表達式表明:輸出X等於輸入A和B的布爾和(OR),讀作“X等於A或B”。
為了計算X=A+B,先看看該式是如何描述或門運算的,將1或0代人每個變數。兩個變數共有2 =4種輸入狀態組合 。
當A=0,B=0: X=A+B=0+0=0;
當A=0,B=1: X=A+B=0+1=1;
當A=1,B=0: X=A+B=1+0=1;
當A=1,B=1: X=A+B=1+1=1。
(2)3輸人或門運算的布爾代數表達式為:
 布爾加法
布爾加法遍歷所有可能的輸入狀態組合(2 =8),代人二進制數值,計算其輸出結果。對應的真值表參見表2。
| A | B | C |  布爾加法 布爾加法 |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |