定義
布爾切換網的動力學表示如下
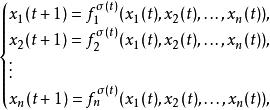 切換布爾網
切換布爾網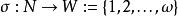 切換布爾網
切換布爾網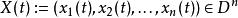 切換布爾網
切換布爾網其中 為切換信號, 為邏輯狀態,
 切換布爾網
切換布爾網為邏輯函式。
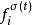 切換布爾網
切換布爾網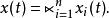 切換布爾網
切換布爾網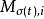 切換布爾網
切換布爾網套用邏輯變數的向量形式並令假設的邏輯矩陣為
利用半張量積理論,可以將上述動態方程組轉化為
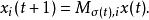 切換布爾網
切換布爾網將上式的每個子式乘積可以得到動態方程組的代數表達式如下
 切換布爾網
切換布爾網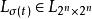 切換布爾網
切換布爾網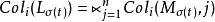 切換布爾網
切換布爾網其中 為系統的狀態轉移矩陣,並且有 。
多模態切換現象成因
在實際基因調控網路的動態行為中,多模態切換時常出現。這種多模態切換現象主要由以下下方而的因素所導致:
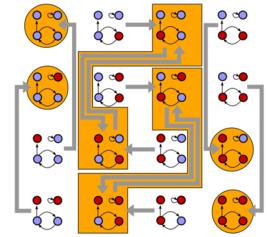
(1)系統自身所同有的屬性.例如,真核細胞的生長和分裂由四個模態構成,每一個模態都由某些離散事件激發所引起(參見圖1).在細胞的分化模型中,由於Delta-Notch蛋自的相互作用,系統的動態演化也呈現多模態切換;.
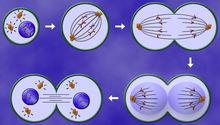 圖1.真核細胞的生長和分裂
圖1.真核細胞的生長和分裂(2)試圖重構給定網路的外部干擾或控制.D. Laschov等在文獻 中指出,通過將控制輸入編碼成切換信號,一個布爾控制網路可轉化為布爾切換系統;
(3)網路進化的異步行為也會產生多模態切換.文獻 指出,通過排列所有可能的布爾函式,一個確定性異步布爾網路可以轉化為切換布爾網路。
研究難點
(1)切換布爾網路的狀態與控制取值只有有限個點,狀態空間是一個有限集,人們很難定義一個公共的距離來衡量所有布爾網路的收斂特性;
(2)切換布爾網路是一個切換信號和離散邏輯狀態並存的混雜系統,每個子模態都是由布爾差分方程所確定的強非線性系統由於用米處理一般切換系統的工具大都只適用於普通的加法和乘法運算,這就使得它們很難被用來處理切換布爾網路中的邏輯加和邏輯乘等運算;
(3)布爾網路的函式的概念尚未被提出,因此依賴於Lyapunov函式的共同Lyapunov函式法和多重Lyapunov函式法無法直接用來研究切換布爾網路。
研究成果
李海濤、王玉振等人建立了一套採用矩陣半張量積理論框架研究切換布爾網路的分析與控制問題的方法,主要研究了該類系統的能控性、穩定性等基本分析問題,並基於此研究系統的鎮定控制、干擾解耦控制、最優控制等控制問題,建立一套適用於切換布爾網路的分析與控制方法 。
基於矩陣半張量積的研究方法同時把所得到的研究結果套用於細胞調控網路的分析與控制、組合電路的故障診斷和有限域網路的趨同分析中。