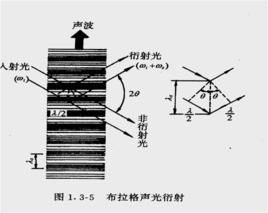
介紹
布拉格衍射(又稱 X射線衍射的布拉格形式),最早由威廉·勞倫斯·布拉格及威廉·亨利·布拉格於1913年提出,他們早前發現了固體在反射X射線後產生的晶體線(與其他物態不同,例如液體),而這項定律正好解釋了這樣一種效應。他們發現,這些晶體在特定的波長及入射角時,反射出來的輻射會形成集中的波峰(叫 布拉格尖峰)。布拉格衍射這個概念同樣適用於中子衍射及電子衍射。中子及X射線的波長都於原子間距離(~150pm)相若,因此它們很適合在這種長度作“探針”之用。
布拉格條件
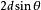 布拉格衍射
布拉格衍射 布拉格衍射
布拉格衍射當電磁輻射或亞原子粒子波的波長,與進入的晶體樣本的原子間距長度相若時,就會產生布拉格衍射,入射物會被系統中的原子以鏡面形式散射出去,並會按照布拉格定律所示,進行相長干涉。對於晶質固體,波被晶格平面所散射,各相鄰平面間的距離為 d。當被各平面散射出去的波進行相長干涉時,它們的相位依然相同,因此每一波的路徑長度皆為波長的整數倍。進行相長干涉兩波的路徑差為,其中為散射角。由此可得 布拉格定律,它所描述的是晶格中相鄰晶體平面(由米勒指數 h、 k及 l標記),產生相長干涉的條件:
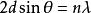 布拉格衍射
布拉格衍射,
其中 n為整數,按各項參數大小而定,而λ則為波長。通過量度散射後入射波的強度,並將之表示成入射角的函式,可得干涉圖樣。在干涉圖樣中,當散射波滿足布拉格條件,就會產生非常強的強度,它們叫布拉格尖峰。
膠體晶體的布拉格可見光散射
膠體晶體為一種非常有序的粒子陣列,可以在大範圍內形成(長度從幾微米到幾毫米不等),而且可被看作原子及分子晶體的類比。球狀粒子的周期性陣列,會形成出相似的空隙陣列,而這種陣列可被用作可見光的衍射光柵,尤其是當空隙與入射波長為同一數量級的時候。
因此,科學家們在很多年前就發現了,由於相斥庫侖相互作用的關係,水溶液中的帶電荷高分子,會表現出大範圍的類晶體相互關聯,當中粒子間距一般會比粒子直徑要大得多。在自然的所有這種例子中,都可到看到一樣的漂亮構造色(或晃動的色彩),這都可以歸功於可見光波的相長干涉,而此時光波會滿足布拉格條件,跟結晶固體的X射線衍射類似。
選擇定則與實驗晶體學
就跟上文提過的那樣,布拉格定律可用於計算某立方晶系的晶格間距,關係式如下:
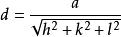 布拉格衍射
布拉格衍射其中a為立方晶體的晶格間距,而h、k及l則為布拉格平面的密勒指數,將上式與布拉格定律結合可得:
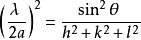 布拉格衍射
布拉格衍射。
我們可以推導出各種不同立方布拉維晶格的密勒指數選擇定則;以下是其種幾種晶格的選擇定則。
| 布拉維晶格 | 化合物例子 | 可行反射 | 不可行反射 |
| 簡單立方 | 釙、氯化鉀 | 任何h、k、l | 無 |
| 體心立方 | 鐵、鎢、鉭、鉻 | h+k+l為偶數 | h+k+l為奇數 |
| 面心立方 | 銅、鋁、鎳、氯化鈉、氫化鋰、硫化鉛 | h、k、l皆為奇數或偶數 | h、k、l當中有奇數也有偶數 |
| 金剛石型 | 硒化鋅、氯化銅、碘化銀、氟化銅、矽、鍺 | 皆為奇數,或皆為偶數且h+k+l= 4n | 同上,或皆為偶數但h+k+l≠ 4n |
| 三角點陣 | 鈦、鋯、鎘、鈹 | l為偶數或h+ 2k≠ 3n | l為奇數且h+ 2k= 3n |
這些選擇定則可用於對應晶體結構下的任何晶體。儘管氯化鈉呈現面心立方的結構,但是由於氯離子跟鈉離子的大小相近,因此衍射圖樣實質上跟簡單立方結構一致,只是各項晶體參數都小了一半。其他結構的選擇定則可在各種相關的參考文獻中找到,也可以自行推導出來。
另見
•晶格
•衍射
•分散式布拉格反射器
•光纖布拉格光柵
•亨德森極限
•衍射的動力學理論
•勞厄方程
•粉末衍射
•結構因子
•威廉·勞倫斯·布拉格
•X射線晶體學