簡介
常微分方程是含有未知函式及其導數的方程，差分方程中含有未知函式及其差分，但不含有導數，微分差分方程是同時含有未知函式及其導數和差分的方程。它同時具有常微分方程和差分方程的特點，而以二者作為特殊情況。從歷史發展看，微分差分方程的產生和發展並不是二者形式上的推廣，而是來自許多不同學科的實際問題。
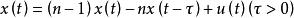差分微分方程對一個物理或技術系統，往往要考慮時間延遲的作用。例如在火箭控制理論中，燃燒室壓力x(t) 的運動方程為 ，壓力的變化率x(t)不僅依賴於當時的壓力x(t),而且明顯的依賴於過去的壓力狀況x(t-τ)，τ稱為時滯，它反映了燃料從射進燃燒室到即將燃燒的臨界狀態需要一段時間。這個方程是一種簡單的含常數偏差變元的微分方程。
考慮含多個時滯的微分差分方程
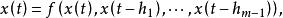差分微分方程
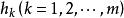差分微分方程
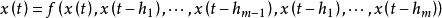差分微分方程式中，時滯 為常數，如果這些常數全為正，稱方程為滯後型方程；如果全為負，則稱為超前型方程。若方程右端有導數的滯後項 稱為中立型方程。對於高階方程或方程組也有類似的分類。
發展歷史
20 世紀30 年代起對偏差變元微分方程進行了系統的研究。
貝爾曼和庫克(Bellman and Cooke,1963)，埃利斯戈爾茨(EI’sgol’tz,1964) 總結了1960 年以前的成果。
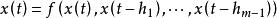差分微分方程
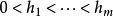差分微分方程
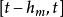差分微分方程50 年代末H.H.克拉索夫斯基(Krasovskii 1959) 把偏差變元微分方程放到函式空間來考慮，如方程 中的偏差滿足條件 ，則方程右端可看成是 上函式x(·) 的泛函，從而微分差分方程成為推動泛函微分方程發展的基本原型。微分差分方程特別是滯後型方程在物理學、力學、控制理論與技術，以及生物學、經濟學領城都有廣泛的套用。
初值問題
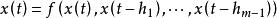差分微分方程 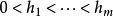差分微分方程
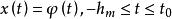差分微分方程
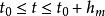差分微分方程
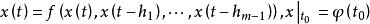差分微分方程滯後型方程 （其中 ）在時刻t₀的初值問題是在初值條件 ，下求t>t₀的解x(t)。通過把這個問題化為常微分方程的分步法，可以討論解的存在性、唯一性問題，並對簡單的方程逐步求解。在區間 上等價的常微分方程初值問題為 。
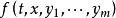差分微分方程
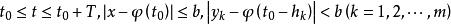差分微分方程
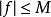差分微分方程
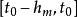差分微分方程
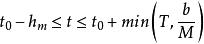差分微分方程 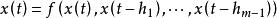差分微分方程 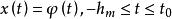差分微分方程
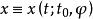差分微分方程設 在 連續，且 ，φ(t)是區間 上的連續函式，則在區間 上方程 存在滿足初值條件 的連續解 。
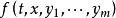差分微分方程
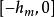差分微分方程
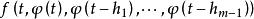差分微分方程
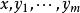差分微分方程
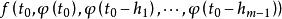差分微分方程若 對 上每一個φ(t)，函式 是連續的，且 f關於 在 的小鄰城內滿足利普希茨條件，則上述解是唯一的，並且解關於初值函式φ是連續依賴的。用不動點定理和格朗瓦爾(Gronwall)不等式可以證明上述存在性和唯一性。對於中立型方程，也可以用分步法求解，但初值函式φ應該是可微的。
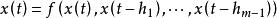差分微分方程 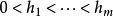差分微分方程
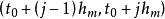差分微分方程
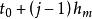差分微分方程若 f關於變數有足夠多次的連續導數，滯後型方程的解在向右開拓時，光滑度增加，若，x³(t)在上連續，而在處一般有第一類間斷；至於向左邊開拓，即使是一階方程也不一定可能。
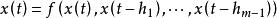差分微分方程
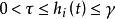差分微分方程若式中時滯hᵢ為t的連續函式，，τ，γ為常數，以上的存在唯一性的結論仍然成立。
