層次分析簡介
 層次分析
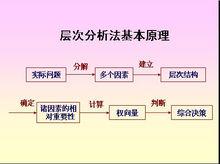
層次分析(AHP)是將決策總是有關的元素分解成目標、準則、方案等層次,在此基礎之上進行定性和定量分析的決策方法。該方法是美國運籌學家匹茨堡大學教授薩蒂於本世紀70年代初,在為美國國防部研究"根據各個工業部門對國家福利的貢獻大小而進行電力分配"課題時,套用網路系統理論和多目標綜合評價方法,提出的一種層次權重決策分析方法。這種方法的特點是在對複雜的決策問題的本質、影響因素及其內在關係等進行深入分析的基礎上,利用較少的定量信息使決策的思維過程數學化,從而為多目標、多準則或無結構特性的複雜決策問題提供簡便的決策方法。尤其適合於對決策結果難於直接準確計量的場合。
層次分析法的基本思路與人對一個複雜的決策問題的思維、判斷過程大體上是一樣的。不妨用假期旅遊為例:假如有3個旅遊勝地A、B、C供你選擇,你會根據諸如景色、費用和居住、飲食、旅途條件等一些準則去反覆比較這3個候選地點.首先,你會確定這些準則在你的心目中各占多大比重,如果你經濟寬綽、醉心旅遊,自然分別看重景色條件,而平素儉樸或手頭拮据的人則會優先考慮費用,中老年旅遊者還會對居住、飲食等條件寄以較大關注。其次,你會就每一個準則將3個地點進行對比,譬如A景色最好,B次之;B費用最低,C次之;C居住等條件較好等等。最後,你要將這兩個層次的比較判斷進行綜合,在A、 B、C中確定哪個作為最佳地點。
步驟
1、建立層次結構模型。在深入分析實際問題的基礎上,將有關的各個因素按照不同屬性自上而下地分解成若干層次,同一層的諸因素從屬於上一層的因素或對上層因素有影響,同時又支配下一層的因素或受到下層因素的作用。最上層為目標層,通常只有1個因素,最下層通常為方案或對象層,中間可以有一個或幾個層次,通常為準則或指標層。當準則過多時(譬如多於9個)應進一步分解出子準則層。
2、構造成對比較陣。從層次結構模型的第2層開始,對於從屬於(或影響)上一層每個因素的同一層諸因素,用成對比較法和1—9比較尺度構造成對比較陣,直到最下層。
3、計算權向量並做一致性檢驗。對於每一個成對比較陣計算最大特徵根及對應特徵向量,利用一致性指標、隨機一致性指標和一致性比率做一致性檢驗。若檢驗通過,特徵向量(歸一化後)即為權向量:若不通過,需重新構造成對比較陣。
4、計算組合權向量並做組合一致性檢驗。計算最下層對目標的組合權向量,並根據公式做組合一致性檢驗,若檢驗通過,則可按照組合權向量表示的結果進行決策,否則需要重新考慮模型或重新構造那些一致性比率較大的成對比較陣。
優點
運用層次分析法有很多優點,其中最重要的一點就是簡單明了。層次分析法不僅適用於存在不確定性和主觀信息的情況,還允許以合乎邏輯的方式運用經驗、洞察力和直覺。也許層次分析法最大的優點是提出了層次本身,它使得買方能夠認真地考慮和衡量指標的相對重要性。
模型
將問題包含的因素分層:最高層(解決問題的目的);中間層(實現總目標而採取的各種措施、必須考慮的準則等。也可稱策略層、約束層、準則層等);最低層(用於解決問題的各種措施、方案等)。把各種所要考慮的因素放在適當的層次內。用層次結構圖清晰地表達這些因素的關係。
〔例1〕 購物模型
某一個顧客選購電視機時,對市場正在出售的四種電視機考慮了八項準則作為評估依據,建立層次分析模型。
〔例2〕 選拔幹部模型
假設有三個幹部候選人y、y 、y,按選拔幹部的五個標準:品德,才能,資歷,年齡和民眾關係,構成層次分析模型。
成對比較矩陣
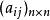 層次分析
層次分析比較第 i 個元素與第 j 個元素相對上一層某個因素的重要性時,使用數量化的相對權重aij來描述。設共有 n 個元素參與比較,則A=稱為成對比較矩陣。成對比較矩陣中aij的取值可參考 Satty 的提議,按下述標度進行賦值。a在 1-9 及其倒數中間取值。
a = 1元素 i 與元素 j 對上一層次因素的重要性相同;
a = 3元素 i 比元素 j 略重要;
a = 5元素 i 比元素 j 重要;
a = 7 元素 i 比元素 j 重要得多;
a = 9元素 i 比元素 j 的極其重要;
 層次分析
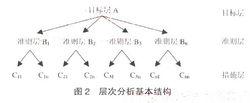
層次分析a = 2n,n=1,2,3,4元素 i 與 j 的重要性介於a = 2n − 1與a = 2n + 1之間;
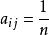 層次分析
層次分析,n=1,2,...,9 若且唯若aij = n。
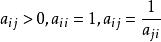 層次分析
層次分析成對比較矩陣的特點:。
對例 2, 選拔幹部考慮5個條件:品德x,才能x,資歷x,年齡x,民眾關係x。某決策人用成對比較法,得到成對比較陣如下:
a = 5 表示品德與年齡重要性之比為 5,即決策人認為品德比年齡重要。
一致性檢驗
從理論上分析得到:如果A是完全一致的成對比較矩陣,應該有aa = a。
但實際上在構造成對比較矩陣時要求滿足上述眾多等式是不可能的。因此退而要求成對比較矩陣有一定的一致性,即可以允許成對比較矩陣存在一定程度的不一致性。
由分析可知,對完全一致的成對比較矩陣,其絕對值最大的特徵值等於該矩陣的維數。對成對比較矩陣 的一致性要求,轉化為要求:的絕對值最大的特徵值和該矩陣的維數相差不大。
檢驗成對比較矩陣 A 一致性的步驟如下:
計算衡量一個成對比矩陣 A (n>1 階方陣)不一致程度的指標CI:
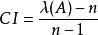 層次分析
層次分析其中λ是矩陣 A 的最大特徵值。註解
從有關資料查出檢驗成對比較矩陣 A 一致性的標準RI:RI稱為平均隨機一致性指標,它只與矩陣階數 有關。
按下面公式計算成對比較陣 A 的隨機一致性比率 CR:
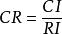 層次分析
層次分析。
判斷方法如下:當CR<0.1時,判定成對比較陣 A 具有滿意的一致性,或其不一致程度是可以接受的;否則就調整成對比較矩陣 A,直到達到滿意的一致性為止。
例如對例 2 的矩陣
層次分析法
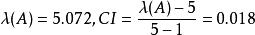 層次分析
層次分析計算得到,查得RI=1.12,
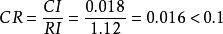 層次分析
層次分析。
這說明 A 不是一致陣,但 A 具有滿意的一致性,A 的不一致程度是可接受的。
此時A的最大特徵值對應的特徵向量為U=(-0.8409,-0.4658,-0.0951,-0.1733,-0.1920)。這個向量也是問題所需要的。通常要將該向量標準化:使得它的各分量都大於零,各分量之和等於 1。該特徵向量標準化後變成U = (0.4759,0.2636,0.0538,0.0981,0.1087) 。經過標準化後這個向量稱為權向量。這裡它反映了決策者選拔幹部時,視品德條件最重要,其次是才能,再次是民眾關係,年齡因素,最後才是資歷。各因素的相對重要性由權向量U的各分量所確定。
求A的特徵值的方法,可以用 MATLAB 語句求A的特徵值:〔Y,D〕=eig(A),Y為成對比較陣 的特徵值,D 的列為相應特徵向量。
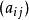 層次分析
層次分析在實踐中,可採用下述方法計算對成對比較陣A=的最大特徵值λmax(A)和相應特徵向量的近似值。
定義
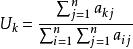 層次分析
層次分析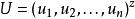 層次分析
層次分析,
可以近似地看作A的對應於最大特徵值的特徵向量。
計算
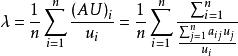 層次分析
層次分析可以近似看作A的最大特徵值。實踐中可以由λ來判斷矩陣A的一致性。
決策
現在來完整地解決例 2 的問題,要從三個候選人yyy中選一個總體上最適合上述五個條件的候選人。對此,對三個候選人y = y1,y2,y3分別比較他們的品德(x),才能(x),資歷(x),年齡(x),民眾關係(x)。
先成對比較三個候選人的品德,得成對比較陣
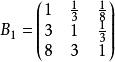 層次分析
層次分析經計算,B的權向量
ωx1(Y) = (0.082,0.244,0.674)
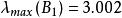 層次分析
層次分析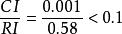 層次分析
層次分析,CI=0.001,
故B的不一致程度可接受。ω(Y)可以直觀地視為各候選人在品德方面的得分。
層次分析法
類似地,分別比較三個候選人的才能,資歷,年齡,民眾關係得成對比較陣
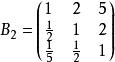 層次分析
層次分析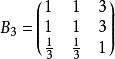 層次分析
層次分析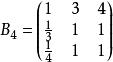 層次分析
層次分析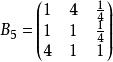 層次分析
層次分析通過計算知,相應的權向量為
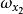 層次分析
層次分析(Y)=(0.606,0.265,0.129)
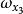 層次分析
層次分析(Y)=(0.429,0.429,0.143)
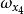 層次分析
層次分析(Y)=(0.636,0.185,0.179)
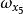 層次分析
層次分析(Y)=(0.167,0.167,0.667)
它們可分別視為各候選人的才能分,資歷分,年齡分和民眾關係分。經檢驗知BBBB的不一致程度均可接受。
最後計算各候選人的總得分。y1的總得分
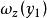 層次分析
層次分析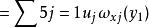 層次分析
層次分析=0.457×0.082+0.263×0.606+0.051×0.429+0.104×0.6366+0.126×0.167=0.305
從計算公式可知,y的總得分ω(y)實際上是y各條件得分ω(y) ,ω(y) ,...,ω(y),的加權平均,權就是各條件的重要性。同理可得y,y 的得分為
ωz(y) = 0.243,ω(y) = 0.452
比較後可得:候選人y是第一幹部人選。

