原理
對稱算法的加密和解密表示為:
Ek(M)=C
Dk(C)=M
對稱算法可分為兩類。一次只對明文中的單個位(有時對位元組)運算的算法稱為序列算法或序列密碼。另一類算法是對明文的一組位進行運算,這些位組稱為分組,相應的算法稱為分組算法或分組密碼。現代計算機密碼算法的典型分組長度為64位――這個長度大到足以防止分析破譯,但又小到足以方便作用。
這種算法具有如下的特性:
Dk(Ek(M))=M
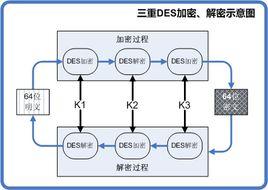
常用的採用對稱密碼術的加密方案有5個組成部分(如圖所示)
l)明文:原始信息。
2)加密算法:以密鑰為參數,對明文進行多種置換和轉換的規則和步驟,變換結果為密文。
3)密鑰:加密與解密算法的參數,直接影響對明文進行變換的結果。
4)密文:對明文進行變換的結果。
5)解密算法:加密算法的逆變換,以密文為輸入、密鑰為參數,變換結果為明文。
特點
對稱密碼術的優點在於效率高(加/解密速度能達到數十兆/秒或更多),算法簡單,系統開銷小,適合加密大量數據。
缺陷
儘管對稱密碼術有一些很好的特性,但它也存在著明顯的缺陷,包括:
l)進行安全通信前需要以安全方式進行密鑰交換。這一步驟,在某種情況下是可行的,但在某些情況下會非常困難,甚至無法實現。
2)規模複雜。舉例來說,A與B兩人之間的密鑰必須不同於A和C兩人之間的密鑰,否則給B的訊息的安全性就會受到威脅。在有1000個用戶的團體中,A需要保持至少999個密鑰(更確切的說是1000個,如果她需要留一個密鑰給他自己加密數據)。對於該團體中的其它用戶,此種倩況同樣存在。這樣,這個團體一共需要將近50萬個不同的密鑰!推而廣之,n個用戶的團體需要N2/2個不同的密鑰。
通過套用基於對稱密碼的中心服務結構,上述問題有所緩解。在這個體系中,團體中的任何一個用戶與中心伺服器(通常稱作密鑰分配中心)共享一個密鑰。因而,需要存儲的密鑰數量基本上和團體的人數差不多,而且中心伺服器也可以為以前互相不認識的用戶充當“介紹人”。但是,這個與安全密切相關的中心伺服器必須隨時都是線上的,因為只要伺服器一掉線,用戶間的通信將不可能進行。這就意味著中心伺服器是整個通信成敗的關鍵和受攻擊的焦點,也意味著它還是一個龐大組織通信服務的“瓶頸”