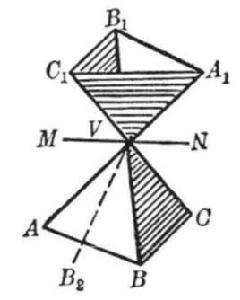
基本概念
對稱多面角是兩個特殊相關的多面角，互為中心對稱、軸對稱、鏡面對稱的多面角的統稱。兩多面角中，如果一個是另一個的中心對稱圖形、軸對稱圖形、鏡面對稱圖形，則分別稱它們是互為中心對稱、軸對稱、鏡面對稱的多面角，或者分別說一個多面角是另一個多面角的中心對稱、軸對稱、鏡面對稱多面角，統稱一個是另一個的對稱多面角。成軸對稱的兩個多面角，可以通過空間繞軸旋轉使一個與另一個重合，而成鏡面對稱或中心對稱的兩個多面角常需要除平移和旋轉外再作一次鏡面反射才能使一個與另一個重合，因此，對稱的兩個多面角總是相等的，其中，只有軸對稱多面角才是同向相等的 。
還有的書對對稱多面角的定義是這樣的：
（1）如果兩個面數相同的多面角，它們對應的面角和二面角分別相等，但排列的順序相反，這兩個多面角，叫做對稱多面角。（2）如果把多面角S-ABCD的各棱經過它的頂點S向反向延長，就構成另一個多面角S-A'B'C'D'，這樣的兩個多面角S-ABCD和S-A'B'C'D'是關於S點為對稱的。在關於某點對稱的兩個多面角中，各對應的二面角相等，各對應的面角也相等，但是在一個多面角中的面角和二面角的位置順序和它的對稱多面角中的對應面角和二面角的位置順序恰好相反 。
顯然這兩個定義說的是“中心對稱多面角”。
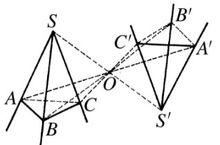圖1 兩中心對稱三面角
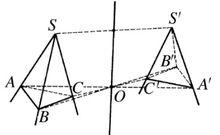圖2 兩軸對稱三面角
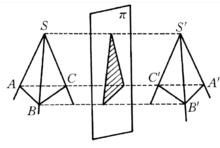圖3 兩鏡面對稱三面角相關結論
定理 兩個對稱多面角是成鏡照相等，但不一定全等 。
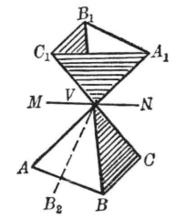圖4如圖4中，多面角V-ABC和多面角V-A₁B₁C₁是對稱多面角，MN是∠CVA₁的平分線，如果把多面角V-A₁B₁C₁繞著MN為軸翻轉一個平角，則棱VA₁和VC相重合，棱VC₁和VA相重合，且兩個面角A₁VC₁和AVC相重合。
但是二面角VA₁不一定等於二面角VC，因此二面角VA₁也就不一定能和二面角VC重合，所以平面A₁VB₁也不一定和平面CVB重合，同樣地兩個平面C₁VB₁和AVB也不一定重合，因而棱VB₁可以落到另一個位置如VB₁，但和VB不相重合。
可知：兩個多面角V-ABC和V-A₁B₁C₁，雖然它們是成對稱，但它們的對應部分卻不一定都處處重合，也就是這兩個多面角不一定是全等的。
關於這一點，我們可以想像到常用的手套，可以把兩隻手套排成對稱形，但是如果要把它的一隻套在另一隻上面，由於手心、手背以及五個指頭的順序不同，是不可能的。
只有兩個面數相同的正多面角，它們既是成對稱(即鏡照相等)，又是全等的 。
