理想氣體狀態方程
理想氣體的假設：
1、氣體分子本身所占的體積比起整個氣體體積來說是可以忽略不計；
2、所有氣體分子間的碰撞以及分子與器壁的碰撞是純彈性的；
3、氣體分子之間以及分子和容納它的器壁之間不存在引力或排斥力。
對於以上條件下的，稱之為理想氣體，它將遵守如下定律：
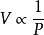天然氣狀態方程波義爾定律： 或PV=C（當T為常數時）
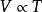天然氣狀態方程
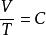天然氣狀態方程蓋·呂薩克定律： 或 （當P為常數時）
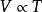天然氣狀態方程
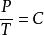天然氣狀態方程查理定律： 或 （當V為常數時）
根據以上定律可推導出理想氣體狀態方程為：
天然氣狀態方程范德華方程式
對於實際氣體來說，除低壓條件下近似服從理想氣體狀態方程式外，一般都與理想氣體狀態方程式發生偏差，有時甚至發生較大的偏差。
這是因為實際氣體的分子間具有作用力。在低壓時，分子與分子間距離較大，作用力可以忽略不計。當處於高壓時，分子間的距離縮短了，其相互間作用力已經不能忽略。
對於理想氣體曾假設分子本身的體積比起總體積來小到可以忽略不計，這在壓力很低時，可以近似地認為是這樣。然而實際上當氣體密度隨壓力增高而增大時，分子所占的體積就不能忽略不計了。
范德華考慮了實際氣體的上面兩種情況，對理想氣體狀態方程式進行了修正：
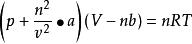天然氣狀態方程式中
a、b是取決於氣體類型的常數。
實用氣體狀態方程
在高壓下必須對理想氣體狀態方程進行修正, 即引入一係數Z, 從而得到天然氣的壓縮狀態方程為:
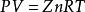天然氣狀態方程式中, Z 通常稱為壓縮因子, 它是給定壓力和溫度下, 實際氣體占有的體積與相同壓力和溫度下的理想氣體所占有的體積之比。
實際氣體由於分子本身具有體積, 故較理想氣體不易壓縮; 而分子間的引力又使實際氣體較理想氣體易於壓縮。壓縮因子Z 的大小恰恰反映出這兩個相反因素的綜合結果。當Z 值大於1 時, 即氣體較理想氣體難壓縮; 而當Z 值等於1時, 實際氣體成為理想氣體。Z 值大小與氣體性質、溫度和壓力有關, 通常必須用實驗測出, 做成圖版備查, 也可以用相關式計算。
套用
對應狀態定律在氣體參數計算中套用也相當廣泛。其內容是: 在相同的對應溫度和對應壓力下, 所有的純烴氣體具有相同的壓縮因子。這裡的對應溫度和對應壓力是指氣體的溫度與壓力分別除以該氣體的臨界溫度和臨界壓力所得的比值。
