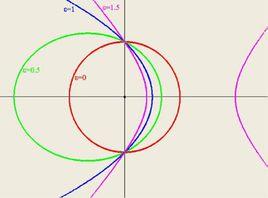
偏心率
偏心率用來描述軌道的形狀,用焦點間距離除以長軸的長度可以算出偏心率。偏心率一般用e表示。e=c/a。
橢圓兩焦點間距離和長軸長度的比值。即某一橢圓軌道與理想圓環的偏離,長橢圓軌道“偏心率”高,而近於圓形的軌道“偏心率”低。
軌道偏心率的變化極其重要,它是制約各類(不同高度)空間飛行體軌道壽命的關鍵因素之一·對於地球低軌衛星,主要受大氣耗散作用的影響,而對環月(或環火星)低軌衛星,主要受非球形引力位中奇次帶諧項的影響,會出現變幅較大的長周期變化,從而導致近星點高度hp在一段時間內有明顯的下降趨勢·對大偏心率軌道和高軌道,第三體的引力作用也會使e出現變幅較大的長周期變化,近星點高度也會有明顯下降的現象,這都會影響衛星的軌道壽命。
星上軌道計算
衛星星上軌道的計算方法通常有解析法和數值積分法等。對於快自轉天體,如地球和火星,由於其非球形引力位中諧項的振動頻率與衛星運動頻率相當,會給構造大偏心率軌道解析解帶來無法克服的困難,因此解析法只適用於偏心率較小(e<0.6)的軌道。採用數值積分方法,要做到較高精度的軌道計算,需要考慮較高階次的形狀攝動以及其他各種攝動因素影響,從而導致計算量較大,若星上計算機復位或切機,數值積分方法將會中斷。
切比雪夫多項式作為一種多項式擬合方法,廣泛用於MEO(中地球軌道)、IGSO(傾斜地球同步軌道),GEO(地球靜止軌道)等軌道。該擬合法實際上是對探測器軌跡的擬合,探測器運動越慢,軌道變化越小,擬合精度越高.對於大偏心率橢圓軌道,由於探測器在近拱點附近運動很快,軌道變化很大,因此該弧段的擬合精度較低。目前有文獻利用精密軌道提供的探測器位置擬合切比雪夫多項式係數,進而實現圓軌道的星上軌道計算,但該方法用於大偏心率橢圓軌道時將會帶來較大的擬合誤差。胡少春等通過引入精密軌道與二體軌道的位置差,利用位置差擬合切比雪夫多項式係數,可以大大提高擬合精度,很好地解決大偏心率橢圓軌道的星上軌道計算問題。
初軌確定
初軌確定是各類太空飛行器發射任務中的一項重要工作,特別是在太空飛行器人軌、變軌控制結束以及軌道維持結束後,都需要進行初軌確定,及時給出人軌根數或控後軌道根數,以判定太空飛行器是否準確入軌或是否進人控後目標軌道,為制定或修改後續飛行控制計畫提供依據,也為後續測控站(船)實施目標捕獲提供準確的引導數據源。
通常太空飛行器人軌、變軌控制結束後能用於定軌的數據弧段都很短,一般入軌段外測數據只有數十秒至幾分鐘,變軌控制結束後也只有幾分鐘的測軌數據。如何使用這么少的測軌數據儘可能定出比較準確的軌道,是國內航天測控領域和有關院校、研究單位的科技人員致力研究的問題。傳統的及其改進的初軌確定方法,在國內航天測控領域已經使用了多年,也基本能滿足任務的需要。然而,以往我國發射的太空飛行器的運行軌道偏心率一般小於0.8,並且變軌時機一般也不選擇在近地點附近,因此測控站可以提供比較長時間的測控支持,亦即可以用於軌道計算的數據弧段較長,基本可以滿足初軌確定的精度要求。隨著我國航天事業的發展,特別是某些新型號任務運行軌道設計採用超大偏心率軌道,以往的初軌確定方法使用短弧段的測軌數據進行初軌確定,其精度很難滿足要求,並且隨著偏心率的增加定軌誤差急劇增加。因此,如何適應新型號任務的特殊需要,研究一種能夠滿足超大偏心率(如接近於0.9)的新方法,是一個非常值得研究的課題。
中國衛星海上測控部的茅永興等提出的新方法是針對某些特殊型號任務軌道偏心率超大(接近於0.9)而造成老的初軌確定方法定軌誤差偏大的特殊情況而提出的,它在初軌計算時融人了軌道改進的思想,明顯地提高了超大偏心率軌道短弧段初軌計算的精度,較好地解決了工程中的實際問題,是一種值得推廣的定軌方法。