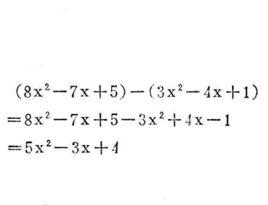基本介紹
多項式的加減法法則：加上一個多項式，依次加上這個多項式的各項；減去一個多項式，改變減式各項的符號，把它們依次加在被減式上。
整式的加減法屬於運算，而運算的依據是法則。因為整式包括單項式和多項式兩部分，所以法則又分為單項式的加減法法則和多項式加減法法則 。
例題解析
【例1】求3m與2m一5的和.
解: 3m+(2m－5)
=3m+2m－5
=5m－5
【例2】求8x²－7x+5與3x²－4x+1的差。
解: (8x²－7x+5)－(3x²－4x+1)
=8x²－7x+5－3x²+4x－1
=5x²－3x+4
單項式的加減法法則
單項式的加減法法則：幾個單項式相加減，只要用加減號把它們連結起來，再合併同類項 。
【例3】求單項式5x²、﹣2x²、 ﹣3x的和。
解 5x²+(﹣2x²)十(﹣3x)
=5x²－2x²－3x
=3x²－3x
【例4】求單項式﹣3xy與﹣7xy的差。
解:﹣3xy－(﹣7xy)
=﹣3xy+(+7xy)
=﹣3xy+7xy
=4xy
整式加減計算的其他說明
從以上的四個例子可以看出，整式加減計算的一般步驟是 ：
(1)根據題意列出代數式；
(2)根據去括弧法則去掉括弧；
(3)合併同類項。
不難看出，整式的加減實質上是合併同類項。因此，整式加減的結果還是整式。
整式的加減能用豎式計算。計算的步驟是:
(1)把一個加式或者被減式按照某一個字母的降冪(或升冪)排列成一行，如果有缺項留出空位；
(2)再把其它加式或者減式寫在它的下面，使同類項對齊；
(3)然後相加或相減 。
【例5】求9x²+7－6x與3 +4x²+5x的和。
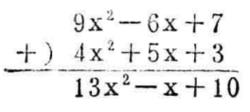多項式加減法法則∴(9x²+7－6x)+ (3+4x²+5x)=13x²－x+10。
【例6】求10m²－7與8－5m的差
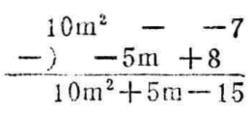多項式加減法法則∴﹣(10m²－7)－(8－5m)=10m²+5m－15 。
