算法描述
夏農–菲諾–以利亞碼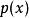
夏農–菲諾–以利亞碼
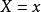夏農–菲諾–以利亞碼給定一離散隨機變數 ，令 為 發生之機率。
定義
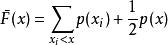夏農–菲諾–以利亞碼算法如下：
對每個X中的x,
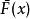夏農–菲諾–以利亞碼令Z為 之二次展開
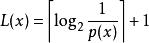夏農–菲諾–以利亞碼令x之編碼長度
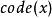夏農–菲諾–以利亞碼
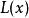夏農–菲諾–以利亞碼選定x之編碼， 為 在Z之小數點後之第一個最高有效位。
算法舉例
令 X = {A, B, C, D} ，其發生機率分別為 p = {1/3, 1/4, 1/6, 1/4}。
（1）對於 A
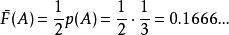夏農–菲諾–以利亞碼在二進制中， Z(A) = 0. 0010101010...
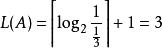夏農–菲諾–以利亞碼code(A) 為 001
（2）對於 B
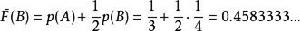夏農–菲諾–以利亞碼在二進制中， Z(B) = 0. 01110101010101...
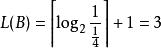夏農–菲諾–以利亞碼code(B) 為 011
（3）對於 C
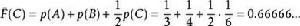夏農–菲諾–以利亞碼在二進制中， Z(C) = 0. 101010101010...
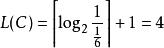夏農–菲諾–以利亞碼code(C) 為 1010
（4）對於 D
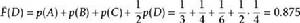夏農–菲諾–以利亞碼在二進制中， Z(D) = 0. 111
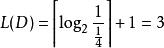夏農–菲諾–以利亞碼code(D) 為 111
算法分析
前綴碼
夏農–菲諾–以利亞碼之輸出為二進制前綴碼，因此可被直接解碼。
令 bcode(x) 為二進制表示法最左側加入小數點而成之小數。舉例而言， code(C)=1010 ，則 bcode(C) = 0.1010。 對所有 x ，如果沒有任何 y 存在使得
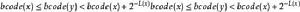夏農–菲諾–以利亞碼則所有的碼可構成前綴碼。
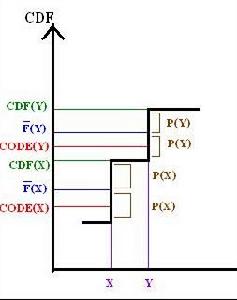圖1 編碼圖解此性質可透過比較 F 和 X 之累積分布函式，以圖1表示出：
由 L 之定義可得
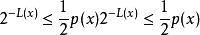夏農–菲諾–以利亞碼並且由於 code(y) 是由 F(y) 從 L(y) 之後的位元截短而得，故
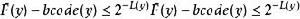夏農–菲諾–以利亞碼因此 bcode(y) 必不比 CDF(x) 小。
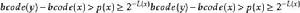夏農–菲諾–以利亞碼上圖說明了 ，因此前綴碼定理成立。
編碼長度
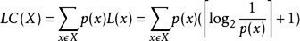夏農–菲諾–以利亞碼此碼之平均長度為。
因隨機變數 X 之熵H(X) 滿足
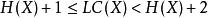夏農–菲諾–以利亞碼夏農–菲諾–以利亞碼之長度約比代編碼資料之熵長約一到二額外位元，故甚少被實用。
