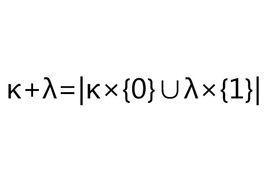基數加法

基數加法(addition of cardinal numbers)是自然數加法的超窮推廣，是定義在基數類上的二元運算。兩個基數κ與λ的和，指將κ的元素與λ的元素合併起來構成的集合的基數，即κ+λ=|κ×0∪λ×1|，基數的加法運算滿足交換律與結合律 。

基本介紹

基數加法是自然數加法的超窮推廣，定義在基數類上的二元運算f：card²→card，若對任意的〈κ，λ〉∈card²，有f(κ，λ)=|κ×{0}∪λ×{1}|，則f稱為基數的加法運算，f(κ，λ)稱為κ與λ的和，記為κ+λ，若A，B為集合，|A|=κ，|B|=λ，A∩B=∅，則κ+λ=|A|+|B|=|A∪B|   。

基數加法的性質

基數加法有下列性質，對任意基數κ，λ，μ：

1.κ+0=κ；

2.κ+λ=λ+κ；

3.(κ+λ)+μ=κ+(λ+μ).；

4.κ·(λ+μ)=κ·λ+κ·μ；

5.若基數κ與λ中至少有一個是無窮基數，則κ+λ=max(κ，λ)。

基數的加法可推廣到任意一個基數集上去。

設{α}是由基數α作成的集合，定義

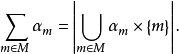基數加法

亦可定義為

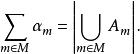基數加法

這裡集族{A}中的元兩兩不相交，且對任何m∈M有|A|=α。

6.對於互不相交集合的族{A}與{B}，若對所有m∈M，有|A|=|B|，則  

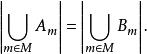基數加法

7.若對所有m