基本介紹
基數乘方是自然數乘方的超窮推廣,設|A|=κ,|B|=λ,映射集合A ={f|f:B→A}的基數|A |稱為κ的λ次方,記為κ 。
基數乘方的性質
基數乘方有下列性質,對任意基數κ,λ,μ :
1.κ =κ ·κ ,一般地有:
 基數乘方
基數乘方2.(κ·λ) =κ ·λ ,一般地有:
 基數乘方
基數乘方3.(κ ) =κ .
4.若κ≤λ,則κ ≤λ .
5.若0<λ≤μ,則κ ≤κ .
6.κ =1;1 =1;若κ>0,則0 =0.
 基數乘方
基數乘方 基數乘方
基數乘方7.對於正則基數κ,且λ<κ,有κ = |α| .特別地,當κ是後繼基數時, .此即豪斯多夫公式.
8.若κ是極限基數,λ≥cf(κ),則
 基數乘方
基數乘方 基數乘方
基數乘方9.取 為固定基數:
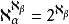 基數乘方
基數乘方1) 若α<β,則 .
 基數乘方
基數乘方 基數乘方
基數乘方2) 若存在γ<α,使 ,則 .
 基數乘方
基數乘方3) 若α>β,且對所有γ<α,有 ,則:
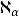 基數乘方
基數乘方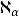 基數乘方
基數乘方 基數乘方
基數乘方 基數乘方
基數乘方① 當 是正則基數或cf( )> 時,有 .
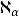 基數乘方
基數乘方 基數乘方
基數乘方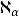 基數乘方
基數乘方 基數乘方
基數乘方 基數乘方
基數乘方 基數乘方
基數乘方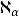 基數乘方
基數乘方 基數乘方
基數乘方 基數乘方
基數乘方② 當cf( )≤ < 時,有 .由此,對任何α與β, 的值為 或 或 (對某個使 成立的γ≤α)。
10.在廣義連續統假設成立時 :
 基數乘方
基數乘方
