介紹
在很多情況下,人們需要對數字圖像進行進一步的處理比如,為了做廣告宣傳,需要將拍攝的藝術照片做成巨幅海報;為了分析深層地質結構,需要對儀器採集的圖像做局部細化;為了分析外星球的大氣和地面狀況,需要使遙感衛星圖片模糊細節變得有意義;為了偵破缺少目擊證人的案件,需要對監控錄像做清晰化處理這些,就需要用到圖像的插值技術,將原始低解析度圖像或模糊圖像進行放大,並且要保證所要求的清晰度有時候,圖像在獲取、傳輸過程中不可避免地會產生噪聲,這些噪聲大大損壞了圖像的質量,影響了圖像的可用性所以,考慮要對圖像進行去噪。而去噪的實質,是在去噪模型下用新的灰度估計值來取代原噪聲點的灰度值,因此去噪問胚也可以轉化為插值問題來研究。
插值,分為圖像內插值和圖像間插值,其主要套用是對圖像進行放大以及旋轉等操作,是根據一幅較低解析度圖像再生出另一幅均具有較高解析度的圖像,是圖像內插值。圖像間的插值,也叫圖像的超解析度重建,是指在一圖像序列之間再生出若干幅新的圖像,可套用於醫學圖像序列切片和視頻序列之間的插值圖像內插值實際上是對單幀圖像的圖像重建過程,這就意味著生成原始圖像中沒有的數據。
種類
傳統的插值方法有:最近鄰插值,雙線性插值,雙平方插值,雙立方插值以及其他高階方法。最近鄰插值和雙線性插值算法很容易出現鋸齒,生成的圖片質量不好。因此一般只在對圖像質量要求不高的場合下採用。雙平方插值和雙立方插值,實質上是”低通濾波器”,在增強圖像平滑效果的同時丟失了許多高頻信息。而在很多套用場合,細節信息恰恰非常重要,要考慮如何在保證平滑效果的同時儘可能地保留細節信息。
最鄰近元法
這是最簡單的一種插值方法,不需要計算,在待求象素的四鄰象素中,將距離待求象素最近的鄰象素灰度賦給待求象素。設i+u, j+v(i, j為正整數, u, v為大於零小於1的小數,下同)為待求象素坐標,則待求象素灰度的值 f(i+u, j+v)。如下圖所示:
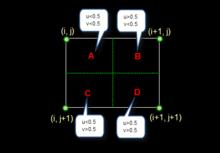 圖象插值
圖象插值如果(i+u, j+v)落在A區,即u<0.5, v<0.5,則將左上角象素的灰度值賦給待求象素,同理,落在B區則賦予右上角的象素灰度值,落在C區則賦予左下角象素的灰度值,落在D區則賦予右下角象素的灰度值。
最鄰近元法計算量較小,但可能會造成插值生成的圖像灰度上的不連續,在灰度變化的地方可能出現明顯的鋸齒狀。
雙線性內插法
雙線性內插法是利用待求象素四個鄰象素的灰度在兩個方向上作線性內插,如下圖所示:
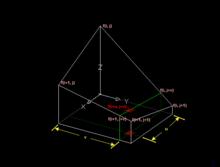 圖象插值
圖象插值對於 (i, j+v),f(i, j) 到 f(i, j+1) 的灰度變化為線性關係,則有:
f(i, j+v) = [f(i, j+1) - f(i, j)] * v + f(i, j)
同理對於 (i+1, j+v) 則有:
f(i+1, j+v) = [f(i+1, j+1) - f(i+1, j)] * v + f(i+1, j)
從f(i, j+v) 到 f(i+1, j+v) 的灰度變化也為線性關係,由此可推導出待求象素灰度的計算式如下:
f(i+u, j+v) = (1-u) * (1-v) * f(i, j) + (1-u) * v * f(i, j+1) + u * (1-v) * f(i+1, j) + u * v * f(i+1, j+1)
雙線性內插法的計算比最鄰近點法複雜,計算量較大,但沒有灰度不連續的缺點,結果基本令人滿意。它具有低通濾波性質,使高頻分量受損,圖像輪廓可能會有一點模糊。
三次內插法
該方法利用三次多項式S(x)求逼近理論上最佳插值函式sin(x)/x, 其數學表達式為:
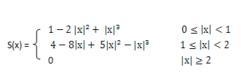 圖象插值
圖象插值待求像素(x, y)的灰度值由其周圍16個灰度值加權內插得到,如下圖:
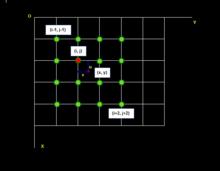 圖象插值
圖象插值三次曲線插值方法計算量較大,但插值後的圖像效果最好。
套用
圖像插值技術廣泛套用于軍事雷達圖像、衛星遙感圖像、天文觀測圖像、地質勘探數據圖像、生物醫學切片及顯微圖像等特殊圖像及日常人物景物圖像的處理。按照套用目的,圖像插值技術的套用場合可歸為以下幾種情況:
(1)在圖像採集、傳輸和現實過程中,不同的顯示設備有著不同的解析度,需要對視頻序列和圖像進行解析度轉換。如:大螢幕顯示圖像和製作巨幅廣告招貼畫。
(2)當用戶需要專注於圖像的某些細節時,對圖像進行放縮變換,如:圖像瀏覽軟體中的放大鏡功能。
(3)在視頻傳輸中,為了有效利用有限的頻寬,可以傳輸低解析度的視頻流,然後在接收端使用插值算法轉換成高解析度視頻流。
(4)為提高圖像的存儲和傳輸效率,而進行圖像的壓縮和重構。如:計算機虛擬現實技術中的圖像差值
(5)在圖像恢復時,已經被損壞的圖像或者有噪聲污染的圖像,可通過插值對圖像進行重建和恢復,如:警方在偵破案件時所發現的存在污損的身份證照片。
