功能
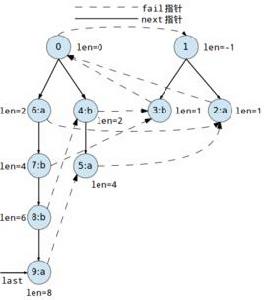
假設我們有一個串S，S下標從0開始，則回文樹能做到如下幾點：
1.求串S前綴0~i內本質不同回文串的個數（兩個串長度不同或者長度相同且至少有一個字元不同便是本質不同）
2.求串S內每一個本質不同回文串出現的次數
3.求串S內回文串的個數（其實就是1和2結合起來）
4.求以下標i結尾的回文串的個數
具體題目：【APIO2014】Palindromes
構造
那么我們該如何構造回文樹？
變數
首先我們定義一些變數。
1.len[i]表示編號為i的節點表示的回文串的長度（一個節點表示一個回文串）
2.next[i][c]表示編號為i的節點表示的回文串在兩邊添加字元c以後變成的回文串的編號（和字典樹類似）。
3.fail[i]表示節點i失配以後跳轉不等於自身的節點i表示的回文串的最長後綴回文串（和AC自動機類似）。
4.cnt[i]表示節點i表示的本質不同的串的個數（建樹時求出的不是完全的，最後count()函式跑一遍以後才是正確的）
5.num[i]表示以節點i表示的最長回文串的最右端點為回文串結尾的回文串個數。
6.last指向新添加一個字母后所形成的最長回文串表示的節點,便於下次insert。
7.s[i]表示第i次添加的字元（一開始設s[0] = -1（可以是任意一個在串s中不會出現的字元））。
8.p表示添加的節點個數。
9.tot表示添加的字元個數。
過程
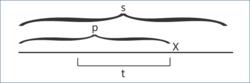build11.對於已經加入的串P（長度可以為0），需再加入一個字元X，構成新串
P‘，t為P的最長回文後綴。
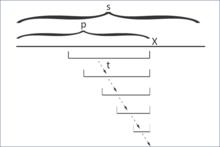build22.我們需要找到P的一條回文後綴A，使得A的左端是一個字元x，因為A本身就是回文串，那么在其左右各加上一個字元x之後仍然是一條回文串，而且，當A長度最長時，形成的回文串xAx就是t'，即P1的最長回文後綴。A可以是空串甚至是長度為-1的串。
3.如果己經有一個結點1代表xAx了，那么我們就將t改成1，退出該過程就行了，否則我們需要新建一個結點，並且還需要加入一條後綴鏈，具體方法也是一樣，繼續沿著後綴鏈找，直到找到符合要求的字元串B為止。
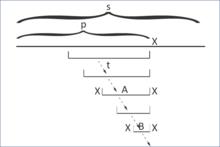build3len設為-1的優越性
我們判定條件字元串A符合要求的條件是這樣:s[Len(p')-Len(A)-1] = s[Len(P')]，當新加入的字元x自己構成一條回文串的時候，Len(A) = -1，我們不需要再加上額外的判定語句。
複雜度
設字元集大小為m，母串長度為n，則空間複雜度為O(nm)，時間複雜度為O(nlogm)[也可以說是O(n)，因為logm極小]
