簡介
四方體法,土方量計算以四方體為計算單元的方格網法。
計算方法
方格四個角點全部為填或全部為挖時V=a2/(H1+H2+H3+H4)為挖方或填方體積(m3);H1、H2、H3、H4為方格四個角點的填挖高度,均取絕對值(m);a為方格邊長。方格四個角點,部分是挖方,部分是填方 。
四稜體的概念
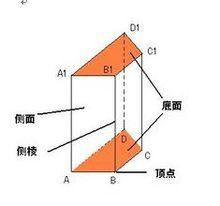 四方體法
四方體法有兩個面互相平行,其餘各面都是四邊形,並且每相鄰兩個四邊形的公共邊都互相平行,由這些面所圍成的幾何體叫做稜柱。稜柱用表示底面各頂點的字母來表示。
四稜柱的概念
稜柱的底面:稜柱中兩個互相平行的面,叫做稜柱的底面。
四稜柱: 底面為四邊形的稜柱是四稜柱。
斜四稜柱:側棱不垂直於底面的四稜柱叫做斜四稜柱。
直四稜柱:側棱垂直於底面的四稜柱叫做直稜柱。
直四稜柱的側棱長與高相等;直四稜柱的側面及經過不相鄰的兩條側棱的截面都是矩形 。
有關直四稜柱的公式
側面積公式:S側=C*h(底面周長*高)
全面積公式:S全=C*h+2*S底面(底面周長*高+2個底面面積)
體積公式:V=S*h(底面面積*高)
其他計算
另外根據格線不同的挖填情況,也會用到四稜台的體積計算:
正四稜台
V=H/3[S1+S2+√(S1S2)]
註:非通用公式,(s1是上底的面積 ,s2是下底的面積 )
四稜台通用公式
V=[S1 + 4S0 + S2] * H / 6
=h/6×[a1×b1+a2×b2+(a1+a2)×(b1+b2)]。
註:上底面積S1,下底面積S2,中截面面積S0,高H, 此體積公式多一個參量S0——中截面積,它有“萬能公式”的美譽。