簡介
四平方數和定理(theorem on the sum of foursquares)亦稱拉格朗日四平方數和定理。四平方數和問題是著名的數論問題.由拉格朗日(La-grange, J.-L.)最終解決，從而有上面的定理名字.該定理斷言:每個正整數均可表為四個整數的平方和(其中有些整數可以為零).
結論
關於表四平方數和的問題有以下結論:
1.兩個四平方數之和的乘積仍是四平方數之和.對此只要證明下列恆等式:設a,b,c,d,r,s,t,u都是整數，則
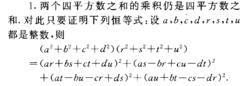四平方數和定理此恆等式的證明很容易，但是發現它卻不那么容易.歐拉(Euler,L.)從1730年首次研究這一問題開始，到1743年發現這個恆等式時，經過了13年的時間.
2.若p是奇素數，且。簇xGp/2,0簇yGpl2，則1-}x2-}yZ=O<modp)必有一組解.
3.對每個奇素數p，必存在一個奇數m,mGp,使方程mp=xZ+yz+zZ+wz有解.
4.若m和p都是奇數，1GmGp，且mp一了+獷+zZ+w2，則存在正整數n,nGm，使np=aZ+bZ+c?+dZ，其中a,b,c,d均為整數。
具體介紹
四平方數之和問題是華林問題的起始命題.177。年，華林(blaring , E.)曾提出，每一個整數是4個平方數之和，9個立方數之和，19個4次方數之和等.但命題“每一個正整數均可表為4個整數的平方和”並非華林最先發現.對此命題的研究有悠久的歷史，遠在公元3世紀末，丟番圖(Diophantus)就已經知道每個正整數可表為四個平方數之和，不過他從未將此結論作為定理明確地敘述出來.梅齊利亞克<Meziriac,C. G. B. de)於1621年出版了附有拉丁譯文和注釋的丟番圖《算術》的希臘文本.書中對四平方數和問題給出了從1到325的數字驗證，說明此命題是正確的，但他未能給出嚴格的證明.費馬(Fermat , P. de)就是在這種版本的丟番圖《算術》書上寫了他的許多著名的頁邊注，他在對此命題的頁邊注中說，他能夠用他的遞降法對此命題作出證明，然而照例地又未提供證明的任何細節.從他對此命題的有關著作來看，費馬的證明是欠完整的.笛卡兒( Descartes , R.)也說過這一定理無疑是正確的，但要找出證明“實在太難了，以至我不敢動手去找”1730年，歐拉開始研究此問題.到1743年，他給出結論:“兩個四平方數之和的乘積仍為四平方數之和”，使本定理的證明向前跨了一大步.直到1770年，拉格朗日(Lagrange,J.-L.)才作出了一個證明.其證明方法基本上是以歐拉的探討線索為依據的.
