概念
第一四分位數 (Q1),又稱“較小四分位數”,等於該樣本中所有數值由小到大排列後第25%的數字。
第二四分位數 (Q2),又稱“中位數”,等於該樣本中所有數值由小到大排列後第50%的數字。
第三四分位數 (Q3),又稱“較大四分位數”,等於該樣本中所有數值由小到大排列後第75%的數字。
第三四分位數與第一四分位數的差距又稱四分位距(InterQuartile Range,IQR)。
示例
首先確定四分位數的位置:
Q1的位置= (n+1) × 0.25
Q2的位置= (n+1) × 0.5
Q3的位置= (n+1) × 0.75
n表示項數
對於四分位數的確定,有不同的方法,另外一種方法基於N-1 基礎。即
Q1的位置=1+(n-1)x 0.25
Q2的位置=1+(n-1)x 0.5
Q3的位置=1+(n-1)x 0.75
Excel 中有兩個四分位數的函式。QUARTILE.EXC 和QUARTILE.INC
QUATILE.EXC 基於 N+1 的方法,QUARTILE.INC基於N-1的方法。
引證:1.minitab軟體自帶“公式與方法”(methods and formulas)
內,關於第一四分位數的原文如下:
1st quartile (Q1)
Twenty-five percent of your sample observations are less than or equal to the value of the first quartile. Therefore, the first quartile is also referred to as the 25th percentile. Q1 is calculated as follows:
let
w = (N+1)/4
y = the truncated integer value of w
z = the fraction component of w that was truncated away
Q1 = x(y) + z(x(y+1) - x(y))
Note: when w is an integer, y = w, z = 0, and Q1 = x(y)
關於第三四分位數的原文如下:
3rd quartile (Q3)
Seventy-five percent of your sample observations are less than or equal to the value of the third quartile. Therefore, the third quartile is also referred to as the 75th percentile. Q3 is calculated as follows:
let
w = 3(N+1)/4
y = the truncated integer value of w
z = the fraction component of w that was truncated away
Q3 = x(y) + z(x(y+1) - x(y))
Note: when w is an integer, y = w, z = 0, and Q3 = x(y)
以上引文中,w代表分位數位置,y代表位置的整數部分,z代表位置的分數部分。
2. 論四分位數的計算 (湖南工學院工商管理系 祁德軍 南華大學數理學院 陳明)
 四分位數
四分位數(原文截圖)
實例1
數據總量: 6, 47, 49, 15, 42, 41, 7, 39, 43, 40, 36
由小到大排列的結果: 6, 7, 15, 36, 39, 40, 41, 42, 43, 47, 49
一共11項
Q1 的位置=(11+1) × 0.25=3, Q2 的位置=(11+1)× 0.5=6, Q3的位置=(11+1) × 0.75=9
Q1 = 15,
Q2 = 40,
Q3 = 43
實例2
數據總量: 7, 15, 36, 39, 40, 41
一共6項
數列項為偶數項時,四分位數Q2為該組數列的中數,Q1為前半組(6項即為前3個數)的中數,Q3為後半組數字的中數,此時
Q1 = 15,
Q2 = (36+39)/2= 37.5,
Q3 = 40.
1、將數據從小到大排序,計為數組a(1 to n),n代表數據的長度
2、確定四分位數的位置:b= 1+(n-1) × 0.25= 2.25,b的整數部分計為c b的小數部分計為d
計算Q1:Q1=a(c)+[a(c+1)-a(c)]*d=a(1)+[a(2)-a(1)] *0.25 =15+(36-15)×(2.25-2)=20.25
3、計算如上 Q2與Q3的求法類似,四分位差=Q3-Q1
套用
不論Q1,Q2,Q3的變異量數數值為何,均視為一個分界點,以此將總數分成四個相等部份,可以通過Q1,Q3比較,分析其數據變數的趨勢。
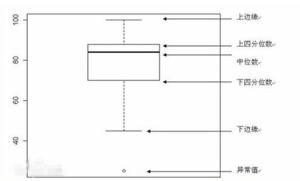
 簡單箱線圖
簡單箱線圖四分位數在統計學中的箱線圖繪製方面套用也很廣泛。所謂箱線圖就是 由一組數據5 個特徵繪製的一個箱子和兩條線段的圖形,這種直觀的箱線圖不僅能反映出一組數據的分布特徵,而且還可以進行多組數據的分析比較。這五個特徵值,即數據的最大值、最小值、中位數和兩個四分位數。即:
相關算法
將n個數從小到大排列:
Q2為n個數組成的數列的中數(Median);
當n為奇數時,中數Q2將該數列分為數量相等的兩組數,每組有 (n-1)/2 個數,Q1為第一組 (n-1)/2 個數的中數,Q3為為第二組(n+1)/2個數的中數;
當n為偶數時,中數Q2將該數列分為數量相等的兩組數,每組有n/2數,Q1為第一組 n/2個數的中數,Q3為為第二組 n/2 個數的中數。