主要原理
如果波長與障礙物相當,衍射現象最明顯.
一,光的衍射,惠更斯—菲涅爾原理
惠更斯原理----介質中波動傳播到的各點,都可看成是發射子波的新波源,在以後的任何時刻,這些子波的包跡就是新的波陣面.
惠更斯原理只能定性解釋波的衍射現象,不能給出波的強度,不能解釋衍射現象中明暗相間條紋的形成.
菲涅耳在惠更斯原理基礎上加以補充,給出了關於位相和振幅的定量描述,提出子波相干疊加的概念.
波在前進過程中引起前方P點的總振動,為面 S 上各面元 dS 所產生子波在 該點引起分振動的迭加.
與 有關.
這樣就說明子波為什麼不會向後退.
面元 dS 所產生的子波在 P 點引起光振動的振幅:
當 =0時,
最大.
當 時
從同一波面上各點發出的子波,在傳播到空間某一點時,各個子波之間也可以互相迭加而產生干涉現象.
這個經菲涅爾發展的惠更斯原理稱為惠更斯—菲涅耳原理
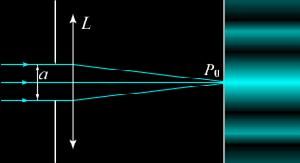
2.夫琅禾費單縫衍射 ----平行光的衍射
計算比較簡單.
光源—衍射孔—接收屏距離為無限遠.
觀察比較方便,但定量計算卻很複雜.
1.菲涅耳衍射----發散光的衍射
光源—衍射孔—接收屏距離為有限遠.
1.菲涅耳與夫琅禾費衍射
二,夫琅禾費單縫衍射
當衍射角 =0時,所有衍射光線從縫面AB到會聚點0都經歷了相同的光程,因而它是同位相的振動.
在O點合振動的振幅等於所有這些衍射線在該點引起的振動振幅之和,振幅最大,強度最大.
2.夫琅禾費單縫衍射
O點呈現明紋,因處於屏中央,稱為中央明紋.
設一束衍射光會聚在在螢幕上某點 P ,它距螢幕中心 o 點為 x,對應該點的衍射角為 .
單縫面上其它各點發出的子波光線的光程差都比AC小.
在其它位置:
過B點作這束光的同相面BC,
由同相面AB發出的子波到P點的光程差,僅僅產生在由AB面轉向BC面的路程之間.
A點發出的子波比B點發出的子波多走了AC=asin 的光程.
每個完整的半波帶稱為菲涅爾半波帶.
菲涅爾半波帶法:
用 / 2 分割 ,過等分點作 BC 的平行線(實際上是平面),等分點將 AB 等分----將單縫分割成數個半波帶.
特點: 這些波帶的面積相等,可以認為各個波帶上的子波數目彼此相等(即光強是一樣的).
每個波帶上下邊緣發出的子波在P點光程差恰好為 /2,對應的位相差為 .
菲涅爾數:單縫波面被分成完整的波帶數目.它滿足:
若單縫縫寬a,入射光波長 為定值,波面能被分成幾個波帶,便完全由衍射角 決定.
若m=2,單縫面,被分成兩個半波帶,這兩個半波帶大小相等,可以認為它們各自具同樣數量發射子波的點.每個波帶上對應點發出的子波會聚到P點,光程差恰好為 /2,相互干涉抵消.此時P點為暗紋極小值處.
依此類推,當m=2k (k=1,2,3… )時,即m為偶數時,屏上衍射光線會聚點出現暗紋.
如果對應於某個衍射角 ,單縫波面AB被分成奇數個半波帶,
分割成偶數個半波帶,
分割成奇數個半波帶,
P 點為暗紋.
P 點為明紋.
結論:
波面AB
按照上面的討論,其中的偶數個半波帶在會聚點P處產生的振動互相抵消,剩下一個半波帶的振動沒有被抵消.
屏上P點的振動就是這個半波帶在該點引起的振動的合成,於是屏上出現亮點,即呈現明紋.
減弱
加強
1.加強減弱條件
2.明紋,暗紋位置
暗紋
明紋
分割成偶數個半波帶,
分割成奇數個半波帶,
P 點為暗紋.
P 點為明紋.
波面AB
討論:
(1)暗紋位置
兩條,對稱分布螢幕中央兩側.
其它各級暗紋也兩條,對稱分布.
(2) 明紋位置
兩條,對稱分布螢幕中央兩側.
其它各級明紋也兩條,對稱分布.
3.中央明紋寬度
中央明紋寬度:兩個一級暗紋間距.
它滿足條件
4.相鄰條紋間距
相鄰暗紋間距
相鄰明紋間距
除中央明紋以外,衍射條紋平行等距.其它各級明條紋的寬度為中央明條紋寬度的一半.
1).
衍射現象明顯.
衍射現象不明顯.
2).
由微分式 看出縫越窄( a 越小),條紋
分散的越開,衍射現象越明顯;反之,條紋向中央靠攏.
當縫寬比波長大很多時,形成單一的明條紋,這就是透鏡所形成線光源的象.顯示了光的直線傳播的性質.
幾何光學是 波動光學在
時的極限情況
結論
特點
主極大
具有相同θ角的屏上部位具有相同的光強,因而屏上的衍射圖樣是一些相互平行的條紋,他們都平行於狹縫。對於θ=0的地方,各衍射光線之間由於沒有光程差而相干加強,因而此處光強最大。最大光強與狹縫寬度的平方成正比,最大光強又稱為主極大或零級衍射斑。
次級大
除了中央主極大外,屏上光強分布還有次級大存在。次級大的位置可同過計算結果為:
α =±1.43π,±2.46π,±3.47π,...
通常把次級大的位置近似表示為
asinθ =±(2k+1)λ / 2 (k = 1,2,3,...)
這些次級大又稱為 高級衍射斑 。
高級衍射斑的強度比中央零級衍射斑的強度小的多。
暗紋位置
暗紋位置滿足關係
asinθ =±kλ(k=1,2,...)
明紋的角寬度
規定相鄰暗紋的角距離為其間明紋的角寬度,即相鄰暗紋間的區域為對應明紋範圍,中央主極大的 半角寬度為
Δθ =λ/a
不難得到各次級大的寬度均相等,均等於中央主極大的半寬度。