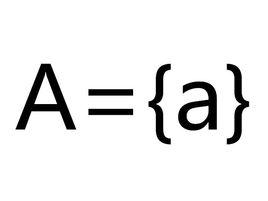基本介紹
單元集亦稱單元素、單元素集，是一種特殊的集合，即只含有一個元素的集合。元素a組成的單元集記為{a}。單元集可看成是無序對集合的特例，即
單元集無序對集合簡稱無序對，又稱無序偶，是一種特殊的集合，即僅含兩個元素的集合。對於任意的兩個對象(集合)u與v，集合{u，v}={v，u}稱為對象u與v的無序對，由於u，v是任意的兩個對象，u與v既可以相同也可以不同，當u=v時，{u，v}可以記為{u}或{v}，集合{u}或{v}稱為單元集，即僅含有一個元素的集合，故單元集是無序對集合的一種特殊情況 。
相關概念
無論是在數學活動中。還是在日常生活中，我們都曾不止一次地使用過“集合”一詞，例如，“小於5的自然數構成的集合”、“某一平面內的所有三角形組成的集合”、“中國的直轄市組成的集合”、“濟源市圖書館的全部藏書組成的集合”等 。
一般地，我們把具有確定性質而相互間又有明確區別的一些對象的全體稱為 集合，簡稱為集，集合中的每個對象叫作這個集合的 元素。
例如，某職業技術學院的全體學生組成一個集合．每個學生都是這個集合的元素；某企業生產的一批電視機(每個個體都被看作是不同的)組成一個集合，其中的任何一台電視機都是這一集合的元素；太陽系的所有行星組成一個集合，每個行星都是這個集合的元素。
通常用大寫字母表示集合，用小寫字母表示元素。例如，常用的一些數集(元素為數的集合)通常用如下字母表示：N表示自然數集，Z表示整數集，Q表示有理數集，R表示實數集。如果上述數集中的元素只限於正數，就在集合記號的右上角標上“+”號；如果數集中的元素都是負數，就在集合記號的右上角標上“-”號。例如，正整數集用N 表示。負整數集用Z 表示，正實數集用R 表示等。
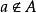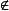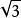單元集
單元集
單元集
單元集 單元集 單元集若a是集合A的元素，就說“屬於A，記作“a∈A”；若a不是集合A的元素，就說a不屬於A，記作“”。例如0∈N，-1N，-2∈Z，∈R，Q，π∈R等，可見數學符號“∈”與“”用來表示元素與集合之間的關係。
包含有限個元素的集合稱為 有限集，不是有限集的集合稱為 無限集。例如，“我國985”某班級學生組成的集合”都是有限集，而自然數集、整數集、有理數集和實數集都是無限集。
我們把不含有任何元素的集合叫作 空集，記作“∅”，讀作“歐”。空集是唯一的，空集是有限集。例如，“方程線x +1=0在實數範圍內的解集”就是空集，我們把至少含有一個元素的集合叫作非空集 。
