發現者介紹
吉伯斯(1839-1903 )出生於康乃狄克新港口市，住在high street,現在位於耶魯大學中心. 1854-1858年在耶魯大學學習,獲學士學位。1863年(美國提供授予博士學位的第3年),在耶魯大學的設菲爾德學院獲得工程學博士學位.1871-1903在耶魯作數學物理學的教授（1871～1880年約翰斯霍普金斯雇用他時沒有工資）。1879年，被選入國家科學協會。
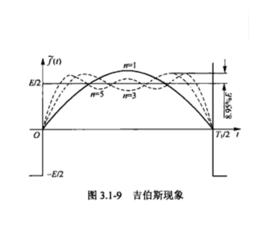
選取傅立葉限級數的項數越多，在所合成的波形中出現的峰值越靠近不連續點。但無論n取的多大（只要不是無限大），峰值均趨於一個常數，它大約等於跳變值8.95%，並從不連續點開始以起伏振盪的形式逐漸衰減下去，這種現象稱為吉伯斯現象 。吉伯斯現象是一種振盪效應，群延遲補償濾波器可能產生這種效應。在具有特性平坦的數字濾波器（一般用於FM套用）的系統中，這種濾波器在波形開始處會出現振盪，其峰值可能比穩定值高20dB。通常，濾波器的這種振盪現象在時域裡出現加新號之後，是由存儲的能量引起的。吉伯斯現象描述的是在這點前的過程 。
發現過程
吉伯斯1902年發表了《統計學基本理論》。1898年,美國物理學家米切爾森(Albert Michelson)做了一個諧波分析儀.該儀器可以計算任何一個周期信號x(t)的傅立葉級數截斷後的近似式 ,其中N 可以算到 80.米切爾森用了很多函式來測試它的儀器 ,結果發現xN(t)都和 x(t)非常一致.然而當他測試方波信號時,他得到一個重要的,令他吃驚的結果!他於是根據這一結果而懷疑起他的儀器是否有不完善的地方.他將這一問題寫了一封信給當時著名的數學物理學家吉伯斯(Josiah Gibbs),吉伯斯檢查了這一結果,並於1899年發表了他的看法.
米切爾森所觀察到的有趣的現象是在不連續點附近部分和 xN(t)所呈現的起伏,這個起伏的峰值大小似乎不隨 N 增大而下降!吉伯斯證明:情況確實是這樣 ,而且也應該是這樣.隨著 N 增加,部分和的起伏就向不連續點壓縮,但是對任何有限的 N 值,起伏的峰值大小保持不變 ,這就是 吉伯斯現象.這個現象的含義是:一個不連續信號x(t)的傅立葉級數的截斷近似 xN(t),一般來說,在接近不連續點處將呈現高頻起伏和超量,而且,若在實際情況下利用這樣一個近似式的話,就應該選擇足夠大的 N ,以保證這些起伏擁有的總能量可以忽略.當然,在極限情況下,近似誤差的能量是零,而且一個不連續的信號(如方波)的傅立葉級數表示是收斂的。
減小方法
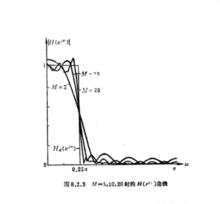M=5,10,20時的H曲線為了減小吉伯斯現象，可以選取一些邊瓣較小的視窗，比如漢寧窗或哈明窗來代替矩形窗。當採用哈明窗，且M=5，10，20時，截取並移位後的h(n)如右圖所示。由圖可知，使用哈明窗後，通帶內的振盪基本消失，阻帶內的紋波也大大減小。從這一點來說，濾波器的性能得到了改善。但是，這是以過渡帶的加寬為代價的 。
現象解釋
圖像的傅立葉變換 ，由於其變換本身有多種成熟的快速算法（FFT算法），而且性能接近於最佳，從而獲得較早的也比較廣泛的研究。它的不足之處在於 ：相鄰子圖像數據在各個邊界不連續造成的所謂Gibbs現像。這是由於圖像數據的二維傅立葉變換實質上是一個二維圖像的傅立葉展開式。當然這個二維圖像應被認為是周期性的。由於子圖像的變換係數在邊界不連續 ，而將造成復原的子圖像在其邊界也不連續 。於是由復原子圖像構成的整幅復原圖像將呈現隱約可見的以子圖像尺寸為單位的方塊狀結構，影響整個圖像質量 。當子圖像尺寸較小時更為嚴重。
解決這個Gibbs現像的方法是後來研究出來的二維餘弦變換（DCT）代替二維傅立葉變換。基本思路為：用一個對稱的2N*2N 像素的子圖像代替原來N*N 子圖像。由於對稱性，子圖像作二維傅立葉變換，其變換係數將只剩下實數的餘弦項。這樣，即可消除Gibbs現像。
偽吉布斯效應
偽吉布斯效應是指不連續點四周的信號會在一個特定目標水平上下波動，是由於信號不連續點位置導致的。
