右因子

亞純函式因式分解F(z)=f(g(z))≡f∘g(z)的分解中，f稱為左因子，g 稱為右因子。

簡介

亞純函式因式分解

亞純函式因式分解是亞純函式在複合意義下的分解。

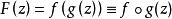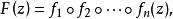右因子

右因子

設F(z)為一亞純函式，若F(z)可表為，f，g為亞純函式；或一般地f(z)(1≤i≤n)皆為亞純函式，以上兩個等式皆稱為F的因式分解或稱分解。

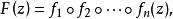右因子

特別地，若F的分解形式中每一個因子關皆為非雙線性亞純函式時，則稱之為一非平凡分解。

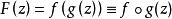左因子

右因子

的分解中，f稱為左因子，g 稱為右因子。

亞純函式

亞純函式是在區域D上有定義，且除去極點之外處處解析的函式。在複分析中，一個複平面的開子集D上的亞純函式是一個在D上除一個或若干個孤立點集合之外的區域全純的函式，那些孤立點稱為該函式的極點。每個D上的亞純函式可以表達為兩個全純函式的比（其分母不恆為0）：極點也就是分母的零點。

直觀的講，一個亞純函式是兩個性質很好的（全純）函式的比。這樣的函式本身性質也很“好”，除了分式的分母為零的點，那時函式的值為無窮。

從代數的觀點來看，如果D是一個連通集，則亞純函式的集合是全純函式的整域的分式域。這和有理數Q和整數Z的關係類似。