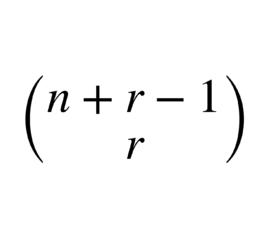簡介
可重組合是一類組合,從非空集合 X={1,2,...,n} 中,每次取出 r 個元素,允許元素重複,且不計順序,這種組合稱為集合 X 的一個 r 可重組合,集合 X 的 r 可重組合的總數為
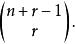 可重組合
可重組合多重集
元素可以多次出現的集合。t=0,1, …∞表示元素a可以出現的次數,含有n個不同元素的多重集可以記為{t·a,t·a…,t·a}。
相關模型
可重組合模型:取r個無標誌的球,n個有區別的盒子,每個盒子允許放多於一個球。
無重組合的模型:n個球是有區別的,r個盒子是無區別的,取r個球放入盒子,每個盒子一個球。
典型問題
線性方程的整數解的個數問題
已知線性方程 x+x+x+...+x=b,n和b都是整數,n≥1,求此方程的非負整數解的個數。
解:
方程的每個非負整數解 (a, a, a,...,a)對應一個將b個無區別的球,放進n個有標誌的盒子(x, x, x,...,x)的情況,允許一盒多於一球,故非負整數的數目等於1到n的正整數取b個作允許重複的組合,其組合數為C(n+b-1,b)。