一元可積函式
可積的條件
（1）可積的必要條件
可積函式類
可積函式類 可積函式類 可積函式類如果函式 在閉區間 上可積，則 是 上的有界函式。
（2）有界函式可積的充分必要條件
可積函式類 可積函式類 可積函式類①上和、下和的定義 設 是閉區間 上的有界函式，T是 的一個分割，記
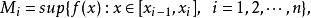可積函式類
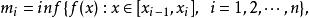可積函式類則稱和數
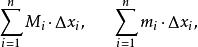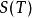可積函式類 可積函式類 可積函式類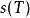
可積函式類
可積函式類分別是 在 上對應於分割T的上和和下和，或稱為達布上和與達布下和，分別記為 與 。
② 有界函式可積的充分必要條件
可積函式類 可積函式類 可積函式類 可積函式類設 是閉區間 上的有界函式，則下述條件都是 在 上可積的充分必要條件：
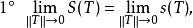可積函式類
可積函式類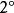
可積函式類 可積函式類對任意 ，存在 的一個分割T，使得
可積函式類
可積函式類 可積函式類 可積函式類對任意 ，存在 的一個分割T，使得
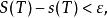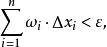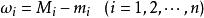可積函式類
可積函式類其中 。
一元可積函式類
可積函式類 可積函式類 可積函式類（1）在閉區間 上的連續函式 在上可積。
可積函式類 可積函式類（2）在閉區間 上只有有限個間斷點的有界函式在 上可積。
可積函式類 可積函式類（3）在閉區間上單調的函式在 上可積。
可積函式類 可積函式類 可積函式類 可積函式類（4）如果函式是 上的有界函式，並且它的間斷點所構成的集合只有有限個聚點，則 在 上可積。
可積函式類 可積函式類 可積函式類
可積函式類 可積函式類 可積函式類 可積函式類（5）如果函式是上的有界函式，並且對於任意 ，總可找出總長不超過 的有限個開區間，把 的全部間斷點覆蓋住，則 在 上可積。
可積函式類（6）在 上可積函式的和、差、乘積仍可積。
例
證明黎曼函式
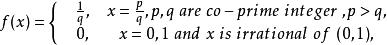可積函式類
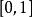可積函式類在區間 上可積。
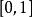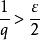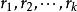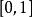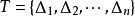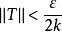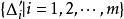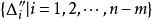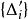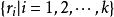可積函式類 可積函式類
可積函式類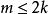
可積函式類
可積函式類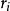 可積函式類
可積函式類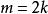
可積函式類
可積函式類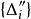
可積函式類
可積函式類
可積函式類
可積函式類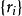
可積函式類
可積函式類
可積函式類
可積函式類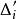
可積函式類
可積函式類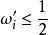
可積函式類
可積函式類證 任給 ，在 上使得 的有理點 只有有限個，設它們為 。現對 作分割 ，使 ，並把T中所有小區間分為 和 兩類。其中 為含有 中點的所有小區間，這類小區間的個數 （當所有 恰好都是T的分割點時才有 ）；而 為 中所有其餘不含 中點的小區間。由於 在 上的振幅 ，於是
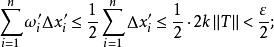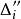可積函式類 可積函式類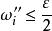
可積函式類
可積函式類而在上的振幅，於是
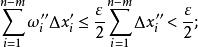可積函式類把這兩部分結合起來，便證得
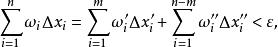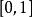可積函式類 可積函式類 可積函式類即在上可積。
二元可積函式
可積的條件
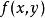可積函式類
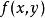可積函式類 可積函式類 可積函式類（1）函式在上可積的必要條件是：在上有界。
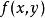可積函式類 可積函式類 可積函式類 可積函式類（2）函式在上的可積的充分必要條件是：對於任意，存在一個分割T，使得
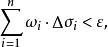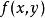可積函式類
可積函式類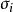 可積函式類
可積函式類其中是在上的振幅（即上、下確界之差）。
二元可積函式類
可積函式類 可積函式類（1）在上連續的二元函式在上可積。
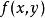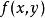可積函式類 可積函式類 可積函式類 可積函式類（2）如果函式在上有界，並且它們的間斷點落在有限光滑曲線段上，則在上可積。
