定義
設函式
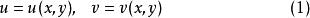 反函式組
反函式組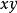 反函式組
反函式組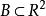 反函式組
反函式組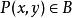 反函式組
反函式組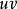 反函式組
反函式組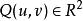 反函式組
反函式組 反函式組
反函式組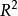 反函式組
反函式組 反函式組
反函式組是定義在平麵點集上的兩個函式,對每一點,由方程組(1)有平面上惟一的一點與之對應。我們稱方程組(1)確定了到的一個映射(變換),記作。這時映射(1)可寫成如下函式形式
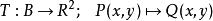 反函式組
反函式組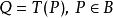 反函式組
反函式組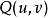 反函式組
反函式組 反函式組
反函式組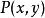 反函式組
反函式組 反函式組
反函式組 反函式組
反函式組 反函式組
反函式組 反函式組
反函式組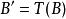 反函式組
反函式組或寫成點函式形式,並稱為映射下的象,而則是的原象。記在映射下的象集為。
 反函式組
反函式組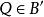 反函式組
反函式組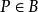 反函式組
反函式組 反函式組
反函式組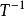 反函式組
反函式組反過來,若為一一映射(即不僅每一原象只對應一個象,而且不同的原象對應不同的象)。這時每一點,由方程組(1)都有惟一的一點與之相對應。由此產生的新映射稱為映射的逆映射(逆變換),記作,即
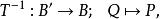 反函式組
反函式組或者
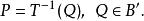 反函式組
反函式組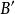 反函式組
反函式組亦即存在定義在上的一個函式組
 反函式組
反函式組把它代入(1)而成為恆等式:
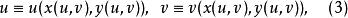 反函式組
反函式組這時我們又稱函式組(2)是函式組(1)的反函式組 。
關於反函式組的存在性問題,其實是隱函式組存在性問題的一種特殊情形。這只需要把方程組(1)改寫成
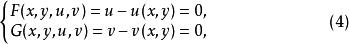 反函式組
反函式組並將隱函式組定理套用於(4),便可得到函式組(1)在某個局部範圍記憶體在反函式組(2)的下述定理。
定理(反函式組定理)
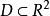 反函式組
反函式組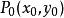 反函式組
反函式組 反函式組
反函式組設函式組(1)及其一階偏導數在某區域上連續,點是的內點,且
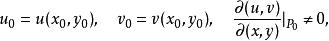 反函式組
反函式組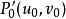 反函式組
反函式組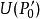 反函式組
反函式組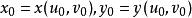 反函式組
反函式組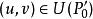 反函式組
反函式組則在點的某一領域上存在惟一的一組反函式(2),使得,且當時,有
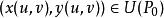 反函式組
反函式組 反函式組
反函式組以及恆等式(3)。此外,反函式組(2)在上存在連續的一階偏導數,且
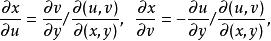 反函式組
反函式組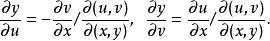 反函式組
反函式組由上式可以看到:互為反函式組的(1)和(2),它們的雅可比行列式互為倒數,即
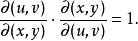 反函式組
反函式組這與(一元)反函式求導公式相類似。
例1
 反函式組
反函式組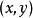 反函式組
反函式組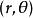 反函式組
反函式組平面上的點的直角坐標與極坐標之間的坐標變換公式為
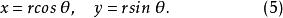 反函式組
反函式組由於
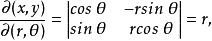 反函式組
反函式組 反函式組
反函式組所以除軸外,在一切點上由函式組(5)所確定的反函式組是
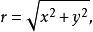 反函式組
反函式組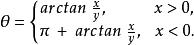 反函式組
反函式組