基本介紹
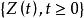 半馬爾科夫過程
半馬爾科夫過程一個半馬爾科夫過程就是依據馬爾科夫鏈改變狀態,但是在變化間消耗時間隨機。更具體地說,考慮一個狀態0,1…時的隨機過程,那就是無論什麼時候它進入狀態i,i≥0;①它將進入的下一個狀態是機率為P的狀態j,i,j≥0;②給出的接下來要進入的狀態是狀態j,從狀態i轉換為狀態j發生的時間已經分配給了F。如果讓Z(t)指示在時間t時的狀態,然後 就稱為一個 半馬爾科夫過程。這樣一個半馬爾科夫過程不會擁有馬爾科夫過程的屬性,即給出的目前狀態的以後是不受過去約束的。在估計以後的時候,想知道的不僅是目前狀態,也包括已經花費在那個狀態上的時長上。
在如下情況里,一個馬爾科夫鏈就是一個半馬爾科夫過程:
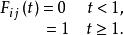 半馬爾科夫過程
半馬爾科夫過程那就是,一個馬爾科夫鏈的所有轉換次數都是1。
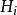 半馬爾科夫過程
半馬爾科夫過程讓表示半馬爾科夫過程在轉換前花在狀態i上的時間分配。也就是說,通過對下一狀態的調節,可以看到:
 半馬爾科夫過程
半馬爾科夫過程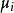 半馬爾科夫過程
半馬爾科夫過程並讓表示它的平均值。也就是,
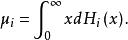 半馬爾科夫過程
半馬爾科夫過程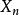 半馬爾科夫過程
半馬爾科夫過程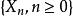 半馬爾科夫過程
半馬爾科夫過程如果讓表示第n個訪問的狀態,然後是一個轉換機率為P的馬爾科夫鏈。它稱為半馬爾科夫過程的嵌入的馬爾科夫鏈。這裡聲明,如果嵌入的馬爾科夫鏈也是不可約的,這個半馬爾科夫過程是不可約的。
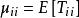 半馬爾科夫過程
半馬爾科夫過程讓T表示依次轉換進狀態i的時間,並讓。通過交替更新流程理論的使用,可以得到一個半馬爾科夫過程的有限機率的表達式。
建議
如果半馬爾科夫過程是不可約的,並且如果T以有限的意思有無結構的分布,然後
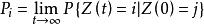 半馬爾科夫過程
半馬爾科夫過程存在並且是不受初狀態約束的,因此有
 半馬爾科夫過程
半馬爾科夫過程驗證
設定不論什麼時候過程進入狀態i,一個循環開始,設定當在系統i內時,過程是開始的,而當不在i內時是關閉的。這樣,就有了一個交替更新流程(當Z(0)≠i時延遲),它的開始時間有分配H,而它的循環時間是T。
推論
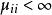 半馬爾科夫過程
半馬爾科夫過程如果半馬爾科夫過程是不可約的,而,然後機率依據表達如下:
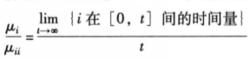 半馬爾科夫過程
半馬爾科夫過程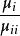 半馬爾科夫過程
半馬爾科夫過程也就是說,等於在狀態i里的長期時間比例 。
相關概念
馬爾科夫分析
馬爾科夫分析(Markov Analysis,MA)是一種用於系統狀態轉移建模和利用該模型計算系統到達各種狀態的機率的分析技術,是一種涉及時序、順序、修理、冗餘和容錯的複雜系統建模工具。MA包括繪製和分析系統狀態轉移圖以確定系統是如何到達不期望的狀態以及計算相應的機率。MA可用於系統性能、可信性、可用性、可靠性以及安全性的建模,描述系統的故障狀態和降級運行狀態,其中降級狀態是指系統或者部分故障,或者只能執行部分功能而其他功能則無法完成。
馬爾科夫鏈(Markov Chain)是系統狀態僅在固定的(離散的)時刻發生改變的隨機過程。然而,日常生活中觀察到的許多物理現象通常都是隨時間連續發生而變化的。這些連續過程的例子有:設備故障、電話的呼叫和輻射衰變等。馬爾科夫過程是系統狀態隨時間連續發生變化的隨機過程,並且未來狀態僅依賴於當前狀態而與過去狀態無關。這一特性為研究系統可靠性、可信性和安全性提供了基本框架。目前有多種類型的馬爾科夫過程,其中半馬爾科夫過程中,兩種狀態轉移之間的時間問隔是一個隨機變數,隨轉移狀況的變化而變化。
為了便於更好地理解MA,需要依次定義一些專用術語。下列是基本的MA術語。
狀態
部件或系統在特定時刻的狀況(例如運行狀態、故障狀態、降級狀態等)。
連線邊
連線或箭頭,用於說明一個部件從一種系統狀態轉移到不同狀態,諸如從運行狀態轉移至故障狀態。
狀態轉移圖
狀態轉移圖是一個表示系統狀態、狀態之間的轉移和轉移率的有向圖。這些圖中包含了足夠信息以便構建狀態方程,用於機率計算。狀態轉移圖是馬爾科夫分析技術的基礎。
組合模型
系統的圖形化表示,基於特定的模型規則在邏輯上將系統部件組合在一起。現用的各種組合模型包括可靠性框圖、故障樹和成功樹。MA中的狀態轉移圖也是組合模型。
確定性過程
確定性過程或模型可由一組給定的條件下得到一個單一的預測結果。一個確定性過程可導出一個確切或肯定的結果,並且在相同的數據條件下可重複得到相同的結果。一個確定性模型是確切的或肯定的,決非隨機的。
隨機過程
一個隨機過程或模型用可能性或機率來預計一組可能的輸出結果。一個隨機過程有一個隨機的或偶然的輸出結果。
馬爾科夫鏈
隨機變數的序列,其中未來的變數依賴於當前變數,而與過去狀態的演變過程無關(對於給定的當前狀態,未來與過去無關)。馬爾科夫鏈假定離散的狀態和離散的時間參數,諸如全局時鐘。
馬爾科夫過程
假定時間是連續的。馬爾科夫過程評價系統從一個已知狀態跳變至下一個邏輯狀態的機率,直至達到最終狀態。例如,第一個狀態是系統正常工作中的任意一種情況,下一個狀態是第一個部件發生故障,然後繼續狀態轉移直至達到系統的故障狀態。這個過程的行為是每個狀態都是無記憶的,意味著系統未來的狀態僅依賴於當前狀態。在靜態系統中,控制系統狀態轉移的機率保持恆定,不隨轉移的發生時刻而變化。

