疊代法
疊代是數值分析中通過從一個初始估計出發尋找一系列近似解來解決問題(一般是解方程或者方程組)的過程,為實現這一過程所使用的方法統稱為疊代法(Iterative Method)。
一般可以做如下定義:
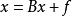 半疊代法
半疊代法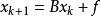 半疊代法
半疊代法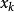 半疊代法
半疊代法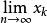 半疊代法
半疊代法對於給定的線性方程組 (這裡的x、B、f 同為矩陣,任意線性方程組都可以變換成此形式),用公式 ( 代表疊代k 次得到的x,初始時k=0)逐步帶入求近似解的方法稱為疊代法(或稱一階定常疊代法)。如果 存在,記為x*,稱此疊代法收斂。顯然x*就是此方程組的解,否則稱為疊代法發散。
跟疊代法相對應的是直接法(或者稱為一次解法),即一次性的快速解決問題,例如通過開方解決方程 x +3= 4。一般如果可能,直接解法總是優先考慮的。但當遇到複雜問題時,特別是在未知量很多,方程為非線性時,我們無法找到直接解法(例如五次以及更高次的代數方程沒有解析解,參見阿貝耳定理),這時候或許可以通過疊代法尋求方程(組)的近似解。
最常見的疊代法是牛頓法。其他還包括最速下降法、共軛疊代法、變尺度疊代法、最小二乘法、線性規劃、非線性規劃、單純型法、懲罰函式法、斜率投影法、遺傳算法、模擬退火等等。
半疊代法的發展
考慮線性方程組
A x = b (1)
其中 A 是 n 階大規模稀疏非奇異實矩陣。由於存儲量和運算量等原因,解決這一類問題的常用方法是疊代方法。疊代法因算法靈活,程式易於實現等原因,已成為求解大規模稀疏線性方程組三大類方法之一 。然而疊代法的收斂性、收斂速度以及它的健壯性等是制約疊代方法有效使用的三大要素。為了使疊代法更加實用有效,對疊代法加速是十分必要的。在眾多的加速方法中,1962年提出的半疊代法(Semi-iterative method)是對疊代法進行加速的一種非常有效的方法,在實際使用中效果非常理想。
研究表明,如果疊代矩陣可對角化,只要疊代矩陣的特徵值分布密集 ,則半疊代法加速效果非常理想。而如果疊代矩陣的最大特徵值接近 1 時,直接採用半疊代加速效果不會太理想。
若干記號和引理
設 n 階矩陣G有 M個相異實特徵值,按模排列為
0 <| λ | <| λ| < ⋯ <| λ | < 1 (2)
其中λ 的重數為 d,i = 1 ,2 , ⋯, M ,滿足 d + d + ⋯ + d= n。
為證明方便,假設虧損陣G為非減次陣,G = SJS 為矩陣G的Jordan分解,其中 S為G的Jordan基矩陣 ,
J = diag( J1 , J2 , ⋯, J m) ,
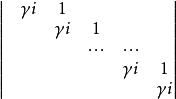 半疊代法
半疊代法J i = , i = 1 ,2 , ⋯, M.
設 Q為次數不超過 m 的所有多項式的集合,則存在pm(x) ∈Qm ,有:
pm(G) = Spm(J)S (3)
其中: pm(J) = diag(pm(J),pm(J) ,⋯,pm (J) ) ,
引理1
假設Tm (z) 是複平面上的次數為m的第一類的Chebyshev 多項式,如果 z ∈[ -1 ,1] ,並 且 0 ≤j≤m ,則 :
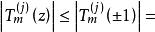 半疊代法
半疊代法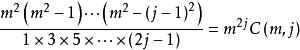 半疊代法
半疊代法如果 j > 1 ,則:
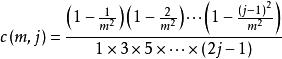 半疊代法
半疊代法隨 j 的增加而減少,並且 C( m ,0) = 1。文中使用的範數均為 2-範數,矩陣的條件數為cond( S) = ‖S ‖‖S ‖ 。
引理2
設
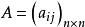 半疊代法
半疊代法則:
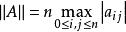 半疊代法
半疊代法半疊代法
設 xˇ = Gxˇ + f , k = 0 ,1 , ⋯ (5)
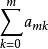 半疊代法
半疊代法為求解線性方程組(1) 的某種疊代方法.,令 x(0) = xˇ (0) ,在疊代格式計算出疊代值x ˇ(0) , xˇ (1) , ⋯,xˇ ( m) 後,選擇滿足 =1的一組常數 a , a , ⋯, a。令:
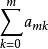 半疊代法
半疊代法x = xˇ,m = 1 ,2 , ⋯
用新的近似 x , x , ⋯, x 作為新的近似解序列。為研究它們的作為近似解的準確程度,引入 μ ( m) =xˇ( m) - xˉ,η= x- xˉ。其 中 xˉ為線性方程組(1) 的準確解 ,即: xˉ= Gxˉ+ f 。由於xˇ = x ,故μ (0) =η (0) ,而:
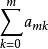 半疊代法
半疊代法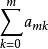 半疊代法
半疊代法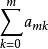 半疊代法
半疊代法η ( m) = xˇ_ xˉ= μ( k)
又:
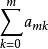 半疊代法
半疊代法μ ( m) = Gμ ( m- 1) = ⋯ = Gμ (0) ,故 η ( m) = { Gk}μ (0) = p(G)η (0) (6)
其中 pm( x) 是滿足 pm (1) = 1的次數不超過 m的多項式。
半疊代法的收斂性
半疊代法計算的近似解的相對誤差滿足:
定理 1
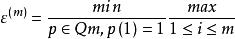 半疊代法
半疊代法設 ‖p(Ji) ‖,
則 ‖ηm‖ ≤cond(S)ε‖η 0 ‖ (7)
證明
利用關係式(6) 、 (3) 和(4) 有 :
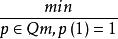 半疊代法
半疊代法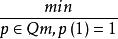 半疊代法
半疊代法‖ηm ‖ ≤ ‖p(G) ‖‖η0‖ = ‖Sp(J)S‖‖η0 ‖ ≤
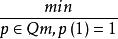 半疊代法
半疊代法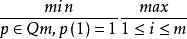 半疊代法
半疊代法cond(S) ‖p(J) ‖‖η 0 ‖ =cond(S) ‖p( Ji) ‖‖η0‖ 。
定理得證。
定理 1 表明
(i) 如果 di = 1 , i = 1 ,2 , ⋯, M ,即矩陣 A 可對角化,關係式(7) 為:
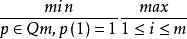 半疊代法
半疊代法‖η‖ ≤cond( S) ‖p‖‖η‖, 這與文獻[1] 中的結論相同。
(ii) 如果矩陣 S 是良態,只要ε 比較小,則近似 解的相對誤差 ‖η ‖必非常小,此時半疊代加速後的近似解 x具有較多的有效數位。
(iii) 如果矩陣 S 是病態,即使ε 非常小, ‖η ‖ 也可能非常大,此時半疊代加速後的近似解收斂將會是非常慢的。
