平衡常數
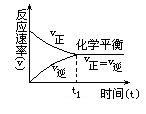可逆反應達到化學平衡
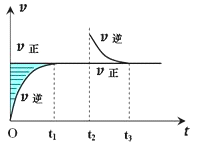平衡常數可逆反應達到化學平衡化學平衡常數，是指在一定溫度下，可逆反應無論從正反應開始，還是從逆反應開始，也不管反應物起始濃度大小，最後都達到平衡，這時各生成物濃度的化學計量數次冪的乘積除以各反應物濃度的化學計量數次冪的乘積所得的比值是個常數，用K表示，這個常數叫化學平衡常數。
反應aA（g）+bB（g）=cC（g）+dD（g）
K=（C濃度的c次方乘D濃度的d次方）除以（A濃度的a次方乘B濃度的b次方）
關於平衡常數的計算與圖像分析
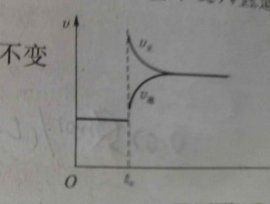
典例：某恆溫密閉容器發生可逆反應Z（?）+W（?）=（可逆）X（g）+Y（?）；ΔH，在t1時刻反應達到平衡，在t2時刻縮小容器體積，t3時刻再次達到平衡狀態後未再改變條件。下列有關說法中不正確的是（B）
A.Z和W在該條件下一定不為氣態
B．t1～t2時間段與t3時刻後，兩時間段反應體系中氣體的平均摩爾質量不可能相等
C．若在該溫度下此反應平衡常數表達式為K=c（X），則t1～t2時間段與t3時刻後的X濃度相等
D．若該反應只在某溫度T0以上自發進行，則該反應的平衡常數K隨溫度升高而增大
平衡移動
在化學反應條件下，因反應條件的改變，使可逆反應從一種平衡狀態轉變為另一種平衡狀態的過程，叫化學平衡的移動。化學平衡發生移動的根本原因是正逆反應速率不相等，而平衡移動的結果是可逆反應到達了一個新的平衡狀態，此時正逆反應速率重新相等（與原來的速率可能相等也可能不相等）。
影響化學平衡移動的因素主要有濃度.溫度.壓強等。
濃度對化學平衡移動的影響
在其他條件不變時，增大反應物的濃度或減小生成物的濃度，有利於正反應的進行，平衡向右移動；增加生成物的濃度或減小反應物的濃度，有利於逆反應的進行平衡向左移動。單一物質的濃度改變只是改變正反應或逆反應中一個反應的反應速率而導致正逆反應速率不相等，而導致平衡被打破。
壓強對化學平衡移動的影響
對於氣體反應物和氣體生成物分子數不等的可逆反應來說，當其它條件不變時，增大總壓強，平衡向氣體分子數減少即氣體體積縮小的方向移動；減小總壓強，平衡向氣體分子數增加即氣體體積增大的方向移動。若反應前後氣體總分子數（總體積）不變，則改變壓強不會造成平衡的移動。壓強改變通常會同時改變正逆反應速率，對於氣體總體積較大的方向影響較大，例如，正反應參與的氣體為3體積，逆反應參與的氣體為2體積，則增大壓強時正反應速率提高得更多，從而是v正>v逆，即平衡向正反應方向移動；而減小壓強時，則正反應速率減小得更多，平衡向逆反應方向移動。
溫度對化學平衡移動的影響
在其他條件不變時，升高反應溫度，有利於吸熱反應，平衡向吸熱反應方向移動；降低反應溫度，有利於放熱反應，平衡向放熱反應方向移動。與壓強類似，溫度的改變也是同時改變正逆反應速率，升溫總是使正逆反應速率同時提高，降溫總是使正逆反應速率同時下降。對於吸熱反應來說，升溫時正反應速率提高得更多，而造成v正>v逆的結果；降溫時吸熱方向的反應速率下降得也越多。與壓強改變不同的是，每個化學反應都會存在一定的熱效應，所以改變溫度一定會使平衡移動，不會出現不移動的情況。
研究歷史
19世紀50-60年代，熱力學的基本規律已明確起來，但是一些熱力學概念還比較模糊，數字處理很煩瑣，不能用來解決稍微複雜一點的問題，例如化學反應的方向問題。當時，大多數化學家正致力於有機化學的研究，也有一些人試圖解決化學反應的方向問題。這種努力除了質量作用定律之外，還有其他一些人試圖從別的角度進行反應方向的探索，其中已有人提出了一些經驗性的規律。
在這一時期，丹麥人湯姆生和貝特羅試圖從化學反應的熱效應來解釋化學反應的方向性。他們認為，反應熱是反應物化學親合力的量度，每個簡單或複雜的純化學性的作用，都伴隨著熱量的產生。貝特羅更為明確地闡述了與這相同的觀點，並稱之為“最大功原理”，他認為任何一種無外部能量影響的純化學變化，向著產生釋放出最大能量的物質的方向進行。雖然這時他發現了一些吸熱反應也可以自發地進行，但他卻主觀地假定其中伴有放熱的物理過程。這一錯誤的論斷在30年代終於被他承認了，這時他才將“最大功原理”的套用範圍限制在固體間的反應上，並提出了實際上是“自由焓”的化學熱的概念。
19世紀60-80年代，霍斯特曼、勒夏特列和范霍夫在這一方面也做了一定的貢獻。首先，霍斯特曼在研究氯化銨的升華過程中發現，在熱分解反應中，其分解壓力和溫度有一定的關係，符合克勞胥斯一克拉佩隆方程：dp/dt=Q/T(V'-V)
其中Q代表分解熱，V、V'代表分解前後的總體積。范霍夫依據上述方程式導出的下式：
lnK=-(Q/RT)+c
此式可套用於任何反應過程，其中Q代表體系的吸收的熱（即升華熱）。范霍夫稱上式為動態平衡原理，並對它加以解釋，他說，在物質的兩種不同狀態之間的任何平衡，因溫度下降，向著產生熱量的兩個體系的平衡方向移動。1874年和1879年，穆迪埃和羅賓也分別提出了這樣的原理。穆迪埃提出，壓力的增加，有利於體積相應減少的反應發生。在這之後，勒夏特列又進一步普遍地闡釋了這一原理。他說，處於化學平衡中的任何體系，由於平衡中的多個因素中的一個因素的變動，在一個方向上會導致一種轉化，如果這種轉化是惟一的，那么將會引起一種和該因素變動符號相反的變化。
然而，在這一方面做出突出貢獻的是吉布斯，他在熱力化學發展史上的地位極其重要。吉布斯在勢力化學上的貢獻可以歸納4個方面。第一，在克勞胥斯等人建立的第二定律的基礎上，吉布斯引出了平衡的判斷依據，並將熵的判斷依據正確地限制在孤立體系的範圍內。使一般實際問題有了進行普遍處理的可能。第二，用內能、熵、體積代替溫度、壓力、體積作為變數對體系狀態進行描述。並指出湯姆生用溫度、壓力和體積對體系體狀態進行描述是不完全的。他倡導了當時的科學家們不熟悉的狀態方程，並且在內能、熵和體積的三維坐標圖中，給出了完全描述體系全部熱力學性質的曲面。第三，吉布斯在熱力學中引入了“濃度”這一變數，並將明確了成分的濃度對內能的導數定義為“熱力學勢”。這樣，就使熱力學可用於處理多組分的多相體系，化學平衡的問題也就有了處理的條件。第四，他進一步討論了體系在電、磁和表面的影響下的平衡問題。並且，他導出了被認是熱力學中最簡單、最本質也是最抽象的熱力學關係，即相律，在，而平衡狀態就是相律所表明的自由度為零的那種狀態。
吉布斯對平衡的研究成果主要發表在他的三篇文章之中。1873年，他先後將前兩篇發表在康乃狄克州學院的學報上，立即引起了麥克斯韋的注意。吉布斯前兩篇文可以說只是一個準備，1876年和1878年分兩部分發表了第三篇文章-《關於復相物質的平衡》，文章長達300多頁，包括700多個公式。前兩篇文章是討論單一的化學物質體系，這篇文章則對多組分復相體系進行了討論。由於熱力學勢的引入，只要將單組分體系狀態方程稍加變化，便可以對多組分體系的問題進行處理了。
對於吉布斯的工作，勒夏特列認為這是一個新領域的開闢，其重要性可以與質量不滅定律相提並論。然而，吉布斯的三篇文章發表之後，其重大意義並未被多數科學家們所認識到，直到1891年才被奧斯特瓦德譯成德文，1899年勒夏特列譯成法文出版之後，情況頓然改變。在吉布斯之後，熱力學仍然只能處理理想狀態的體系。這時，美國人洛易斯分別於1901年和1907年發表文章，提出了“逸度”與“活度”的概念。路易斯談到“逃逸趨勢”這一概念，指出一些熱力學量，如溫度、壓力、濃度、熱力學勢等都是逃逸趨勢量度的標度。
路易斯所提出的逸度與活度的概念，使吉布斯的理論得到了有益的補充和發展，從而使人們有可能將理想體系的偏差進行統一，使實際體系在形式上具有了與理想體系完全相同的熱力學關係式。
綜上所述，化學平衡狀態是指在一定條件下的可逆反應，正反應和逆反應的速率相等，反應混合物中各組分的濃度保持不變的狀態。
基本模型
關於氣體的化學平衡有這兩種基本模型，即一種是等容裝置，另一種是等壓裝置。
具體解釋
對於一個反應Ma+Nb=Qc+Dp其中M，N,Q,D為方程式前的計量數。
第一大類；TV不變，即容積不變時
1.M+N>Q+D或M+N
這個時候只能建立等同平衡，記住這時只能建立等同。
什麼叫等同？顧名思義，就是什麼都是相同的。
這個相同是建立在平衡的基礎上的，平衡是不管你怎么加都是那個百分含量。
2.M+N=Q+D的時候
這個時候可以建立等效平衡
即在平衡時候之前加入的個生成物是按比例生成的
這個時候的各物質濃度會隨著加入的比的變化而變化
但這兩種情況各物質的百分含量是不變的
其實等效平衡你可以理解為平衡時各物質的關係是相同的
第二大類：TP不變即容器的壓強不變
這類的容器一般與活塞相連】
保證了活塞內氣體的作用力不變。
還是這兩類
1.M+N>Q+D或M+N
這種類型的可逆反應。由於壓強是會隨著反應的改變而改變的，但在這種容器中外界的大氣壓力會使反應時刻處於平衡狀態。故這種平衡下什麼都是不變的
如
各物質的濃度百分比
2.M+N=Q+D
這種類型的可以說是以上所有類型的綜合體。就是真正意義上的什麼都不變。他的意義就好像是你進行同一個反應，一個用大碗一個用小碗一樣。
等效平衡
1．等效平衡
（1）定義
同一可逆反應，一定條件下，當改變起始時反應物或生成物物質的量或物質的量濃度，達到平衡時，混合物中各組分的百分組成相等，這樣的平衡稱等效平衡。
（2）產生原因
平衡，只與溫度、壓強和濃度有關，與加料順序無關。
根據氣體狀態方程，pV=nRT，可以發現：如果保持溫度不變，恆容體系，只要“一邊倒”之後，各組分n相同，壓強也相同，平衡狀態也相同。如果保持溫度不變，恆壓體系，只要“一邊倒”之後，各組分n成同一比例，濃度也相同，那么平衡狀態也相同。
2．規律與判斷
（1） 一般可逆反應，恆溫恆容時，當起始反應物或生成物的物質的量通過化學計量數換算相同時，則建立等效平衡。
如反應 2SO₂+O₂=（可逆）=2SO₃ 在（A）、（B）條件時建立等效平衡
（A） 起始時加入：2mol SO₂ + 1mol O₂
（B） 起始時加入：2mol SO₃
注意：此情況下，無論反應物還是生成物，起始時物質的量一定要與化學計量數比相同。
（2） 一般可逆反應，恆溫恆壓時，當起始反應物或生成物的物質的量比（不一定要求與化學計量數比相同）相同時，即建立等效平衡。
如反應 2SO₂+O₂=（可逆）=2SO₃ 在（C）、（D）時建立等效平衡
（C）起始時加入：1mol SO₂ + 1mol O₂
（D）起始時加入：2mol SO₂ + 2mol O₂
（3） 對於反應前後體積不變的氣體反應，恆溫恆容時，當起始反應物或者生成物的物質的量比（不一定要求與化學計量數比相同）相同時，建立等效平衡。
如反應 H₂+I₂（氣） 2HI 在（E）、（F）時建立等效平衡
（E）起始時加入：1mol H₂+2mol I₂
（F）起始時加入：2mol H₂+4mol I₂
3．套用
利用等效平衡原理進行平衡問題分析2例
例1在相同條件下（T=500K），相同體積的甲乙兩容器，甲中充入1mol SO₂和1mol O₂，乙中充入2mol SO₂和2mol O₂，下列敘述中不正確的是（ ）
（A） 反應速率：乙> 甲 （B） 平衡混合物中SO₂的體積分數：乙> 甲
（B）SO₂的轉化率：乙> 甲 （D） 平衡時O₂的體積分數：甲> 乙
簡析
若將乙容器的容積擴大2倍，則甲乙為等效平衡；再將乙容器容積恢復到原體積，則壓強增大，反應速率增大，平衡向生成SO₃的方向移動，故（A）、（C）、（D）項都是正確的，只有（B）項是錯誤的。答案（B）。
例2在一定溫度下，將a molPCl₅通入一容積不變的密閉容器中，達到如下平衡： PCl₅(g)=（可逆）=PCl₃(g)+Cl₂(g) 測得平衡混合氣的壓強為P₁ ；此時，再向此反應器中通入a mol PCl₅，在溫度不變時，重新達到平衡時，測得壓強為P₂，則P₁ 與P₂ 的關係是（ ）
（A）2P₁>P₂ (B) 2P₁P₁
簡析
第二次平衡，可以這樣設計：將容器體積擴大1倍，通入2a mol PCl₅，此時建立的平衡與第一次平衡相同，壓強相等；再將容器體積恢復為原容積，壓強增大，平衡向逆反應方向移動，混合氣總物質的量減小，建立新平衡，即第二次平衡，故 P₁ < P₂ < 2P₁。答案（A、D）。
套用等效平衡原理分析有關化學平衡問題的一般思路：
根據已知條件，先合理變換條件，使之成為等效平衡；然後將體系恢復為原條件，再恢復原條件。
關於等效平衡難點——推“隔板”問題
化學平衡例：在一個容積固定的反應容器中, 有一可以左右滑動的密封隔板, 兩側分別進行如下圖所示的可逆反應:
各物質的起始加入量如下: A、B、C 均為 4.0 mol, D為 6.5 mol, F為 2 mol, 設E 為 x mol, 當x 在一定範圍內變化時, 均可以通過調節反應器的溫度時兩側反應都達到平衡, 且隔板恰好處於反應器的正中位置。
當x = 4.5時, 則右側反應起始時向 正反應,要使起始反應維持向該方向進行, x 的最大值應小於7。
若x 分別為 4.5 和 5.0, 則在這兩種情況下, 當反應達到平衡時, A的物質的量兩種情況下不相同，因為溫度不同。
x = 3.0時, 右側反應在起始時向逆反應, 要使起始反應維持向該方向進行, x 的最小值應大於2.5
x = 4.5時, 左右兩側反應體系達到平衡後, 向左側反應器中充入a mol A氣體, 當左右兩側再次達到平衡狀態時, 則a 的取值範圍為0<2。
等效平衡新題型——等效熱問題
例：已知：① H2(g)+N2(g)+3O2(g) =2HNO3(l)；△H1= —348.2KJ/mol，②2NO(g)= N2(g)+ O2(g);△H2= —180.5 KJ/mol,③3NO2(g)= N2(g)+3O2(g); △H3= —99.6 KJ/mol ④H2O(l)= H2(g)+ O2(g)；△H4= +285.84 KJ/mol，⑤H2O(l)= H2O(g)；△H5= +44.02 KJ/mol，⑥3NO2(g) +H2O(g)=（可逆）2HNO3(l)+ NO(g)；△H6 。在一恆溫恆壓的密閉容器中充入5mol NO2和8mol H2O(g)，記為平衡Ⅰ，達平衡時生成1molNO。相同條件下同一容器中充入xmol NO2，ymol H2O(g)和3molNO，記為平衡Ⅱ，達平衡時，NO的質量分數與平衡Ⅰ相同，且放出熱量115.73KJ，則x=11，y=29。
簡析：△H6= —115.73KJ/mol，算出在平衡Ⅰ平衡時放出熱量115.73KJ，平衡時剩餘NO2：2 mol，H2O（g）：7 mol，NO：1 mol。因為平衡Ⅱ與平衡Ⅰ等效，且放出熱量相同，又因為有3molNO充入，所以需要NO2：2*3=6 mol，H2O(g)：7*3=21 mol維持平衡狀態，再充入與平衡Ⅰ完全相同的NO2、H2O（g）則就與原平衡放出熱相同且等效，所以x=6+5=11 mol，y=21+8=29 mol，這是如今出現的較難的等效平衡問題，一旦與熱聯繫起來就不好建立理想模型了，本題的思考方法值得借鑑。
限度判斷
1.體系中各組分的物質的量的濃度或體積分數、物質的量分數保持不變；
2.全是氣體參加的、前後化學計量數改變的可逆反應，壓強保持不變；
3.全是氣體參加的、前後化學計量數改變的可逆反應，平均相對分子質量保持不變；
4.對於有顏色的物質參加或生成的可逆反應，顏色不隨時間發生變化；
5.對同一物質而言，斷裂化學鍵的物質的量與形成化學鍵的物質的量相等。
6.V正=V逆
