定義
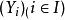 初拓撲
初拓撲 初拓撲
初拓撲給定集合 ,一族拓撲空間 ,與一族映射
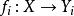 初拓撲
初拓撲 初拓撲
初拓撲 初拓撲
初拓撲上的初拓撲,是使得
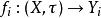 初拓撲
初拓撲均為連續的最粗糙拓撲。
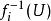 初拓撲
初拓撲 初拓撲
初拓撲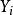 初拓撲
初拓撲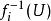 初拓撲
初拓撲 初拓撲
初拓撲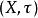 初拓撲
初拓撲更精確地說,初拓撲可以描述為由為子基生成的拓撲,這裡的是中的開集。集合通常也被叫做“圓柱集合”,如果指標集只包含一個元素,那么的全體開集都是圓柱集合。
實例
•子空間拓撲是在子空間上,關於包含映射的初拓撲。
•積拓撲是關於一族投影映射的初拓撲。
•局部凸拓撲向量空間的弱拓撲是關於映射至其對偶空間的連續線性運算元的初拓撲。
性質
特徵性質
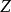 初拓撲
初拓撲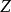 初拓撲
初拓撲 初拓撲
初拓撲 初拓撲
初拓撲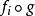 初拓撲
初拓撲給出任意拓撲空間
,X上的初拓撲依照上面所給的定義。則有以下性質成立:從到的映射是連續的,若且唯若是連續的。
從閉集分離點
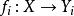 初拓撲
初拓撲 初拓撲
初拓撲 初拓撲
初拓撲 初拓撲
初拓撲 初拓撲
初拓撲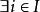 初拓撲
初拓撲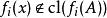 初拓撲
初拓撲稱
從閉集分離點,如果中任意閉集,與任意不屬於的點,,使得這裡的cl是閉包運算元。
 初拓撲
初拓撲關於初拓撲有如下定理:
一族連續映射從閉集分離點,若且唯若the cylinder sets構成集合
 初拓撲
初拓撲 初拓撲
初拓撲 初拓撲
初拓撲從這個定理可以得到,如果上有一族連續映射從閉集分離點,那么關於這族映射就存在一個初拓撲。反之是不成立的,因為初拓撲是由為子基生成的拓撲,在這個定理中要求the cylinder sets是集合的一個基。