列維-辛欽公式

列維-辛欽公式（Levi-Khinchin formula）是描述群X與其對偶群關係的一個重要論斷。

簡介

列維-辛欽公式是描述群X與其對偶群關係的一個重要論斷。

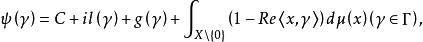列維-辛欽公式

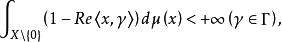列維-辛欽公式

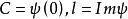列維-辛欽公式

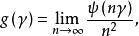列維-辛欽公式

X的對偶群Γ上的一個復值函式ψ是一個具有對稱列維測度的連續負定函式的充分必要條件其中常數C≥0，l是Γ的連續實值同態，g是Γ上非負連續二次型，μ是X\{0}上的正對稱測度且滿足並且，C,l,g,μ由ψ惟一決定，即，μ是關於ψ的列維測度，上述方程稱為列維-辛欽公式。

列維測度

列維測度是在X\{0}上與(μ)相關聯的一個正測度。

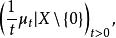列維-辛欽公式

設(μ)是X上的卷積半群，則在X\{0}上的正測度網當t→0時渾收斂於X\{0}上的一個正測度μ，稱μ是關於(μ)的列維測度。

對偶群

若G是局部緊緻阿貝爾群，G的特徵標是一個從G到圓群T的連續群同態；特徵標在逐點乘法下構成一個群，一個特徵標的逆元是它的復共軛。可證明所有G上的特徵標在緊緻開拓撲（即：以緊集上的一致收斂定義收斂性）下構成一個局部緊緻阿貝爾群，稱作對偶群。