簡介
冪律模型的流動方程式,即赫謝爾-布爾克萊模型的流動方程式同 屈服剪下應力τ為零時吻合。因此,冪律流體流速分散式、流量以及平均流速 計算分別在赫謝爾-布爾克萊流體的各個方程式中,如令比栓半徑a=0就可求得。因而,流速分散式、流量以及平均流速可分別表示如下:
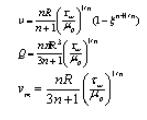 冪律流體
冪律流體具體內容
式中:τ = K*γ^n
τ--剪下應力
K--稠度係數,或稱為冪律係數,單位:Pa·sn
n--流性指數,或稱為冪律指數,無單位
K值是粘度的度量,但不等於粘度值,而粘度越高,K值也越高。
在剪下速率一定範圍內,n值可當作常數處理。
n值是非牛頓性的度量,n值越低或越高曲線也越彎曲,非牛頓性也越強,泥漿n值一般在0.5以下為好。
分類
當n<1時為假塑流體;
當n=1時為牛頓流體;
當n>1時為膨脹流體。
而冪律流體分為假塑流體與膨脹流體。其中最常見的是假塑流體。
性質
一類非牛頓流體。
以下兩種流體均稱冪律流體:
(1)假塑性流體——在穩定的剪下流動下,流體黏性隨剪下速度的增加而減少時的流體(如大多數聚合物,抗菌素溶液)。其特徵為,n<1,式中τ為剪應力,為速度梯度;
(2)脹塑性流體——在穩定剪下流動下,流體黏度隨剪下速率增加而增加時的流體(如澱粉、蔗糖溶液等)。其特徵為,n>1。
研究背景及意義
非牛頓流體力學是近幾十年才興起的流體力學的一個新分支。早在四,五十年代,人們就己經對非牛頓流體在圓管和環空中的Poiseuille流和Couette流做了大量的理論分析和計算。上述研究結果,己成為非牛頓流體力學理論的重要組成部分。我們相信,進一步開展非牛頓流體環空軸向流的研究,會更加豐富非牛頓流體力學的理論寶庫。
套用舉例
用高分子處理劑處理的低固相泥漿及聚合物鑽井液,多屬於假塑性流體,或介於賓漢體與假塑體之間,是冪律流體。
高濃度的澱粉糊、一些礦漿、高固相含量的塗料等都屬於膨脹性流體,也是冪律流體。

