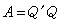共聚合
正文
由兩種或兩種以上單體共同聚合,生成同一分子中含有兩種或兩種以上單體單元的聚合物的反應。其產物為共聚物。兩種單體(M1和M2)單元呈無規分布的共聚物稱無規共聚物,這種共聚反應稱無規共聚。兩種單體單元嚴格呈交替分布的共聚物稱交替共聚物,相應的共聚反應稱交替共聚。如果兩種單體單元各自構成很長的序列(例如有幾百個單體單元的序列),由兩個或兩個以上這種長序列構成的共聚物稱嵌段共聚物。分子的主鏈由一種或一種以上的單體單元構成,而支鏈卻由另一種或一種以上的單體單元構成的共聚物稱接枝共聚物。這四種共聚物可表示為:
對共聚合的套用和研究已經有近50年的歷史,共聚物的分子鏈是由兩種(或多種)單體單元所組成,它的物理力學性能取決於這些單體單元的性質、相對數量和排列情況。因此,利用共聚合可設計和製造出符合人們所要求的性能的聚合物,大大擴充了聚合物的品種和套用領域。例如丁苯橡膠和丁腈橡膠都是共聚物;又如聚苯乙烯是一種抗衝擊和抗溶劑性差的塑膠,使它的套用受到限制,但苯乙烯和丙烯腈的共聚物或它們與聚丁二烯接枝形成的ABS塑膠的韌性就很好,套用領域也廣得多。共聚合的研究還可以測定各種單體、自由基、正碳離子和負碳離子在鏈式聚合中的活性,進一步了解單體活性和化學結構間的關係。
共聚合方程 在大多數情況下,共聚物的組成與生成它的單體物料的組成是不同的,共聚物的組成也不能由兩單體的均聚速率來預測。1944年F.R.梅奧和F.M.路易斯以及 J.Jr.艾爾弗雷和G.戈德芬格幾乎同時分別推導出了表達單體物料組成和共聚物組成之間的定量關係的共聚合方程。
共聚物組成
主要由構成共聚物的兩種單體的聚合速率決定,而單體絕大多數在鏈增長中被消耗。在共聚合中,假設它們的活性鏈(可以是自由基、正碳離子或負碳離子)的化學活性只和鏈末端的那個單體單元有關。如果單體M1和單體M2共聚,就有兩種不同活性的活性鏈,即以M1單體單元結尾的活性鏈M壒和以M2單體單元結尾的活性鏈M壗。在共聚合中有四種增長反應:
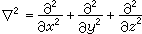
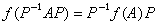
共聚合方程還可以用分子分數的形式表示:
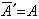
許多實驗事實都證明了共聚合方程的正確性,共聚合方程適用於自由基、正離子和負離子共聚合。由於共聚物組成常與原料單體的組成不同,隨著反應的進行,原料單體組成和生成的共聚物組成在不斷發生變化,因此上述共聚合方程只代表原料單體組成和瞬間生成的共聚物組成間的關係。它只適用於低轉化率下的計算,如果要用原料單體組成計算高轉化率下的共聚物組成,可用有關的積分方程。
1948年E.梅爾茨等人曾提出前末端單元對活性鏈的活性可能有影響,並按八種鏈增長方式推導出更為複雜的共聚合方程。50年代以來,有不少事實證明,相當數量的單體的前末端單元,甚至更遠一些的單元對活性鏈的活性也有影響,特別是高極性的單體(如丙烯腈)、有雙取代基的單體(如馬來酸酐)和具有較大空間阻礙的單體(如α-甲基苯乙烯)。 另外,對存在多種活性種的某些離子型共聚合,其共聚合方程應作相應的變動。
共聚物組成曲線
為了簡便而又清晰地反映原料單體組成和共聚物組成之間的關係,常根據共聚體系的競聚率用f1-F1和f2-F2曲線表示式(1)和(2),這種曲線稱為共聚合組成曲線,它也可以根據實驗數據得出。共聚合組成曲線的形式與共聚體系競聚率有很大關係,下圖給出了有代表性的五類曲線。當r1=r2=1時,為理想共聚特例,此時共聚物組成等於物料的組成 (直線1);而r1>1,r2<1時,則得曲線2,表明M1的共聚傾向大於M2;曲線3則正好相反,r1<1,r2>1,表明M2的共聚傾向大於 M1;當r1<1,r2<1時為曲線4,曲線與對角線相交,交點稱為恆比點,此時共聚物的組成等於物料的組成;當r1≈0,r2≈0時為交替共聚(曲線5)。在很廣的物料配比範圍內都能得到交替共聚物。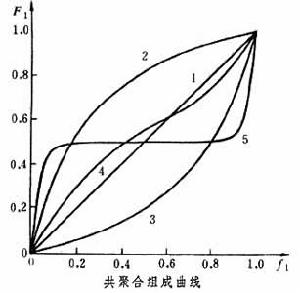 共聚合
共聚合G.E.Ham,Copolymerization,High Polymers,Vol. 18,lnterscience, New York, 1964.