六六幻方

陝西歷史博物館二樓展廳陳列著一塊刻著印度——阿拉伯數碼的鐵板。它是1273年修建安西王府時，壓在房基下，作為避邪、防災的物品。1957年在西安東郊元代安西王府遺址出土的。這個蘊含著數字原理的六六幻方，在古代被視為奇妙的神秘之物。那時，人們已經對“六六幻方”蘊含的數字秘密有了基本了解。主要認識包括以下幾點。
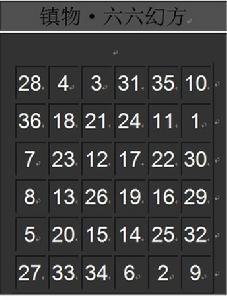
1、每行、每列及兩條對角線上的六個數之和都是111。
2、第一行和第六行六個數字的平方和是相等的，都是3095（28^2+4^2+3^2+31^2+35^2+10^2=27^2+33^2+34^2+6^2+2^2+9^2=3095）；第一列和第六列也是如此，平方和等於2947。這是這塊“六六幻方”非常獨特的地方。
3、 “回整幻方”。去掉“六六幻方”最外一層數字，剩下部分是一個四階幻方，其每行、每列及兩條對角線上的4個數之和都是74。
4、“完美幻方”。即上述四階幻方各條“泛對角線”上的4個數之和也都是74。例如，18+15+19+22、23+21+14+16、11+23+26+14，等。
更為奇特的是，上述四階幻方就是由11-26組成的四階幻方，這個四階幻方還具有以下特點：

第一行和第三行數字的平方和都相等，即18^2+21^2+24^2+11^2=13^2+26^2+19^2+16^2=1462。

第二行和第四行數字的平方和都相等，即23^2+12^2+17^2+22^2=20^2+15^2+14^2+25^2=1446。

第一列和第三列數字的平方和都相等，即18^2+23^2+13^2+20^2=24^2+17^2+19^2+14^2=1422。

第二列和第四列數字的平方和都相等，即21^2+12^2+26^2+15^2=11^2+22^2+16^2+25^2=1486。