發展簡史
大M法與兩階段法都是在原問題缺少初始可行基的情況下利用引人人工變數構造人工基，以達到運用單純形法求解原問題的目的。用大M法處理人工變數，手工計算求解時不會碰到麻煩。但用電子計算機求解時，對M就只能在計算機內輸出一個機器最大字長的數字。如果線性規劃問題中的a、b或c等參數值與這個代表M的數比較接近，或遠遠小於這個數字，由計算機計算時有可能使計算結果發生錯誤，從而使求解的最終結果與原問題真正的最優解不一致。為了克服這個困難，可以對添加人工變數後的線性規劃問題分為兩個階段來計算，而避免M的使用，這個方法稱為兩階段法。
定律定義
兩階段法的方法步驟具體闡述如下，線性規劃LP問題的標準化後的矩陣形式為：
兩階段法
兩階段法在約束條件中加入人工變數 y=(y,y,···,y) 變為 ，人工變數設為x也可。
第一階段
第一階段的就是求解這個目標函式是只包含人工變數的輔助問題。首先構造一個輔助的人工目標函式：令目標函式中其他變數的係數取零，人工變數的係數取某個正的常數（一般取1），在保持原問題約束不變的條件下求這個目標函式極小化的解：
兩階段法
兩階段法
兩階段法也即
兩階段法因為人工變數是虛擬的，在最優時它不應該有取值。如果原問題有可行解，那么人工變數必定取零y=0(i=1, 2, ···,m)，那么輔助問題的最優值一定為z=0。設最優解目標函式值為z，第一階段求解的結果有三種可能的情況：
兩階段法(1)如果第一階段求解結果為z≠0，說明最優解的基變數中含有非零的人工變數，從而表明原問題無可行解，不必進行第二階段，計算終止。
(2)如果第一階段求解結果z=0，如果輔助問題的最優基變數中沒有人工變數，進入第二階段。
(3)如果第一階段求解結果z=0，如果輔助問題的最優基變數中仍有為0的人工變數，這表明原問題有退化的情況，在輔助問題的最優的單純形表中有：
兩階段法
兩階段法其中 為非基變數下標集，這時又分兩種情況：
(i)若a全為0，則人工變數所在行中有原變數（現在是非基變數）下的元素都是0，這表明原問題的約束方程中有多餘的，將其去掉，轉入第二階段。
(ii)若a不全為0，則以a為主元，進行換基疊代，最後轉入轉入第二階段。
第二階段
當第一階段求解結果表明問題有可行解時，第二階段是在原問題中去除人工變數，並由第一階段得到的最優解出發，繼續尋找原問題的最優解。 即在第一階段的最優單純形表中去掉人工變數所在的行列，將價值係數改換成原問題的價值係數，進一步疊代，求解原問題的最優解或者無窮多最優解。
方法套用
鑒於兩階段法求解相對抽象複雜，這裡我們用一個實例演示其求解過程。為了方便讀者進行兩階段法和大M法對比，這裡我們採用和大M法相同的算例進行演示。
兩階段法先將其轉化為標準形式，即
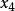兩階段法
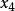兩階段法 兩階段法 兩階段法
兩階段法
兩階段法 兩階段法 兩階段法 兩階段法這裡我們加入了兩個鬆弛變數 和 ,但是此時仍然沒有一個m*m的線性無關矩陣作為初始基底（此時m=3），於是我們看到 代表的列可以作為基底 ，於是我們再加入兩個變數 和 ，從而能夠構成一個基陣。這兩個變數 和 即為 人工變數。
變換後的形式如下：
兩階段法接下來我們要進行第一階段。
第一階段
構造輔助函式
兩階段法列表求解
| C | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 兩階段法 | ||
| C | x | b | P | P | P | P | P | P | P | |
| 0 | x | 4 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 4 |
| 1 | x | 1 | -2 | [1] | -1 | 0 | -1 | 1 | 0 | 1 |
| 1 | x | 9 | 0 | 3 | 1 | 0 | 0 | 0 | 1 | 3 |
| c-z | 10 | 2 | [-4] | 0 | 0 | 1 | 0 | 0 | ||
2入基，6出基。
| C | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 兩階段法 | ||
| C | x | b | P | P | P | P | P | P | P | |
| 0 | x | 3 | 3 | 0 | 2 | 1 | 1 | -1 | 0 | 1 |
| 0 | x | 1 | -2 | 1 | -1 | 0 | -1 | 1 | 0 | - |
| 1 | x | 6 | [6] | 0 | 4 | 0 | 3 | -3 | 1 | 1 |
| c-z | 6 | [-6] | 0 | -4 | 0 | -3 | 4 | 0 | ||
1入基，7出基 (此時其實4出基也可以，但是我們為了儘快把人工變數出基，這裡選擇7出基)
| C | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 兩階段法 | ||
| C | x | b | P | P | P | P | P | P | P | |
| 0 | x | 0 | 0 | 0 | 0 | 1 | -1/2 | -1/2 | -1/2 | |
| 0 | x | 3 | 0 | 1 | 1/3 | 0 | 0 | 0 | 1/3 | - |
| 0 | x | 1 | 1 | 0 | 2/3 | 0 | 1/2 | -1/2 | 1/6 | |
| c-z | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | ||
人工變數全被出基，Z=0，表示最佳化問題有解，進入第二階段。
第二階段
在第一階段的最終表中，去掉人工變數，將目標函式的係數換成原問題的目標函式係數，作為第二階段計算初始表，用單純形法繼續計算。
兩階段法| C | -3 | 0 | 1 | 0 | 0 | 兩階段法 | |||
| C | x | b | P | P | P | P | P | ||
| 0 | x | 0 | 0 | 0 | 0 | 1 | -1/2 | - | |
| 0 | x | 3 | 0 | 1 | 1/3 | 0 | 0 | - | |
| -3 | x | 1 | 1 | 0 | [2/3] | 0 | 1/2 | 3/2 | |
| c-z | -3 | 0 | 0 | [3] | 0 | 3/2 | |||
3入基，1出基
| C | -3 | 0 | 1 | 0 | 0 | 兩階段法 | |||
| C | x | b | P | P | P | P | P | ||
| 0 | x | 0 | 0 | 0 | 0 | 1 | -1/2 | ||
| 0 | x | 5/2 | -1/2 | 1 | 0 | 0 | 1/4 | ||
| 1 | x | 3/2 | 3/2 | 0 | 1 | 0 | 3/4 | ||
| c-z | 3/2 | -9/2 | 0 | 0 | 0 | -3/4 | |||
兩階段法
兩階段法
兩階段法
兩階段法此時檢驗數已經沒有正數，此時,,,, ,
z=3/2。得解。
讀者可以對上述的單純形表和大M法對比，可以發現，大部分的取值是相同的。
套用領域
在大規模線性規劃問題的求解中，通常採用兩階段法運算。
