介紹
兩軍問題是計算機領域的一個思想實驗,用來闡述在一個不可靠的通信鏈路上試圖通過通信以達成一致是存在缺陷的和困難的。這個問題和更有名的“拜占庭將軍問題”有關(譯者註:拜占庭將軍問題很早就被提出,但是沒有普及,後來為了普及,採用故事的方式來說明問題,並命名為拜占庭將軍問題),並且經常出現在計算機網路課程的開頭(特別是由於解釋傳輸控制協定中的TCP協定並不能保證通信兩端狀態的一致性)。不過兩軍問題適用於任何有可能通信失敗情況下的兩點通信。在認知邏輯上一個重要概念是,兩軍問題強調了常識的重要性。也有些學者稱之為“兩軍悖論”、“兩軍難題”、“協同攻擊問題“等。兩軍問題是在計算機通信領域首個被證明無解的問題(譯者註:據說量子通信可能會解決此問題),由此也可推論出,隨機通信失敗條件下的“拜占庭將軍問題”也同樣無解。
定義
兩支軍隊,分別由兩個將軍領導,正在準備攻擊一個堅固的城市。兩支軍隊都駐紮在城市旁邊的兩個不同的山谷里。兩軍之間隔著第三個山谷,兩個將軍想要通訊的唯一方法就是穿過第三個山谷傳送信件。問題是,第三個山谷被城市的守衛軍占據,並且經此傳送的信件可能會被守衛軍截獲。
雖然兩個將軍商量好要同時對城市發起攻擊,但是他們沒有約定特定的攻擊時間。為了保證取勝,他們必須同時發起攻擊,否則任何單獨發起攻擊的軍隊都有可能全軍覆沒。他們必須互相通信來決定一個同時攻擊時間,並且同意在那個時間發起攻擊。兩個將軍彼此之間要知道另一個將軍知道自己同意了作戰計畫。(譯者註:A同意了作戰計畫,A將同意作戰計畫的信發給B,A將軍要知道:B知道了A同意了作戰計畫。)因為返回來的信件和送出去的信件一樣容易丟失,未來大量的訊息必須保持一致性。
這個思想實驗致力於考慮兩軍怎么做才能達成一致。在最簡單的情況下,其中一個將軍作為領導人,決定著發起攻擊的時間,他必須將這個時間準確無誤地通知另外一個將軍。現在的問題是提出一種兩個將軍可以使用的算法。這個算法包含傳送和接收處理訊息,並正確地做出決定和推斷:
沒問題,我們會在約定的時間同時發起攻擊。
考慮到兩個將軍達成同時攻擊的約定非常簡單(例如,每一個成功發出去的信件,必須有一個成功的返回)。兩軍問題的微妙之處在於,對於上面的情形,不可能設計出一種能安全使用的算法。
 兩軍問題
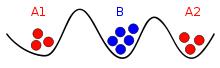
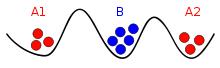
兩軍問題軍隊位置圖。A1和A2軍隊需要通信,但是他們的信息有可能被B軍隊攔截。
問題描述
A1將軍可以先傳送一個訊息:八月4日9點發起攻擊。但是,一旦訊息傳送出去,A1將軍並不知道A2是否收到了這個訊息。這種不確定性使得A1將軍攻擊之前非常猶豫,因為有獨自發起攻擊的危險。
為了讓A1將軍放心,A2將軍可能要傳送一個確認的返回信息給A1將軍:“我收到了你訊息,我會在八月4日9點發起攻擊”。可是,這個給A1將軍的確認訊息也面臨著被守衛軍截獲的可能,A2將軍也猶豫了,如果A1將軍沒有收到確認信息,那么A1將軍很有可能停止此次攻擊。
證明
確定性協定
因為協定是確定性的,假設有一個固定數量訊息的佇列,一些訊息成功傳送了,另一些失敗了。假設兩個將軍有一個明確的攻擊目標。
考慮最後一條訊息成功送達。如果最後一條訊息沒有成功送達,至少有一個將軍(很有可能是接收這條訊息的將軍)估計會不進行攻擊。從最後一條訊息傳送者的角度出發,已傳送的和已送達的訊息佇列順序和預想的一致,並且包含所有已傳送的訊息。
因為協定是確定性的,最後一個傳送訊息的將軍依然決定發起攻擊。這樣會形成如下情形:這個協定讓一個將軍發起攻擊,另一個將軍不發起攻擊。這個情形與這個協定能解決兩軍問題的假設相矛盾。
變長協定
一個帶有變長訊息的不確定性協定就像一個有限的森林,每個葉子或者分支(節點)代表一個被發現的相當於特定點的實例。
森林的根節點標記著第一條合適的訊息。由根節點衍生出來的分支節點標記著合適的下一條訊息。葉子節點代表傳送了最後一條訊息的實例。在傳送任何訊息之前,這個協定就是一棵空樹。
假設有一個不確定性協定可以解決兩軍問題。那么,根據之前確定性協定的場景和分析,可以從一棵樹去掉所有葉子節點,得到另外一棵樹。也就是說,確定性協定一定也可以解決兩軍問題。
因為不確定性協定是有限的,由此可推斷一棵代表空樹的協定,也可以解決兩軍問題。很顯然這是扯淡。所以不存在一個不確定性協定可以解決兩軍問題。
工程方法
一個解決兩軍問題實際可行的辦法就是接受而非試圖去消除通信信道的不可靠性,但是要將這種不可靠性降低到可以接受的程度。例如,A將軍可以送出100個信使,並預期所有信使被抓的可能性是極低的。用了這種方法,A將軍無論如何都會發起攻擊,B將軍只要收到一個信使的信,也會發起攻擊。
一個類似的方法是,A將軍發起一連串訊息,B將軍對每一個訊息都返回一個應答訊息。兩個將軍對每個返回的訊息都感覺是充分的。
但是正如證明里看到的那樣,無法確定攻擊是協調一致的。沒有一種可用的算法(比如收到4個訊息)一定能防止只有一個將軍發起攻擊。
同樣的,A將軍可以給每一個傳送的信息編號,從1到n。這種方法可以讓B將軍了解信道的可靠性,並且傳送適當數量的返回信息來保證至少有一條信息會被收到。如果這個信道是可靠的,一條訊息足夠了,其他的訊息都沒什麼用了。最後一條訊息和第一條訊息一樣容易丟失。
假設每傳送一個訊息並被攔截時,將軍將會犧牲一批士兵,那么我們可以設計這樣一種算法,使得用最少的訊息通信換取協同攻擊的最大化確認。為了達到這個目的,傳送方使用停止傳送信息的方式表示已收到至少一次確認信息並承諾發起攻擊。假設每個訊息通過危險區需要1分鐘,傳送方收到確認信息後沉默200分鐘,這樣可以既不用犧牲更多的士兵又能達到高可靠的協同可信度。也就是說,只有當接收方沒有收到攻擊時間時傳送方才會繼續傳送訊息。傳送方沉默200分鐘後,接收方將得出以下結論:一種可能是連續200個訊息都被敵方截獲(顯然機率極低);另一種可能是對方已收到我的確認信息也相信我將發起攻擊,對方也將發動攻擊。
歷史
兩軍問題及其無解性證明1975年被E. A. Akkoyunlu、K. Ekanadham和R. V. Huber首次提出。發表在《網路通信設計的約束與權衡》一文中。它在73頁的開頭用來描述兩個匪徒團伙之間的通信。
1978年,Jim Gray在《資料庫作業系統筆記》的465頁,將這個問題命名為“兩軍問題”。這個引用被普遍地認為是最早的兩軍問題的定義和無解證明,但是正如上一段說的,其實他們早就被發表了。