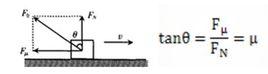
簡介
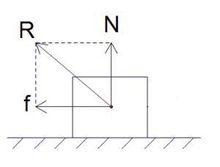全反力的示意圖法向反力（支持力）N與摩擦力F的合力R稱為支持面對物體的全約束力，也叫全反力或接觸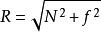反力。
全反力由於支持力N沿支持面法向，摩擦力f沿支持面切向，二者總相互垂直。運用勾股定理，全反力R的大小為。
靜摩擦力f達到最大值fmax時，這時的支持力與全反力的夾角a也達到最大值b,把b稱為最大靜摩擦角。此式表明：最大靜摩擦角b的正切等於最大靜摩擦因數。而動摩擦角的正切等於動摩擦因數。
計算公式
法向反力N與摩擦力F的合力R稱為支持面對物體的全反力。 即摩擦力F達到最大值Fmax時，這時的夾角a也達到最大值b，把b稱為摩擦角。
tanb=F/N=fN/N=f 此式表明：摩擦角b的正切等於靜摩擦因數。 如果作用於物體的主動力的合力Q的作用線在摩擦角之內，則無論這個力怎樣大，總有一個全反力R與之平衡，物體保持靜止；反之，如果主動力的合力Q的作用線在磨擦角之外，則無論這個力多么小，物體也不可能保持平衡。這種與力大小無關而與摩擦角有關的平衡條件稱為自鎖條件。物體在這種條件下的平衡現象稱之自鎖現象。
相關區別
摩擦角：當物體處於滑動的臨界狀態時，靜摩擦力FS達到最大值Fmax,此時FR 與FN 的夾角也最大，此時的φm 稱為摩擦角。物體恰好能從粗糙斜面上勻速下滑時斜面的傾角稱為摩擦角。如果測得這個角度就能確定物體與斜面之間的動摩擦因數，即μ=tanθ。不過用這種方法測定摩擦因數有一定的難度，因為物體是否真正作勻速運動，依靠目力是難以辨別的。我們發現在變速運動的情況下也可以引入摩擦角，只要量出角度就能得到摩擦因數，從而可以避免判定速度是否均勻的困難。
法向反力N與摩擦力F的合力R稱為支持面對物體的全約束力，也叫全反力。法向反力（支持力）N與摩擦力F的合力R稱為支持面對物體的全約束力，也叫全反力或接觸反力 。
套用
自鎖現象
如果作用於物體的主動力的合力Q的作用線在最大靜摩擦角之內，則無論這個力怎樣大，總有一個全反力R與之平衡，物體保持靜止；反之，如果主動力的合力Q的作用線在最大靜摩擦角之外，則無論這個力多么小，物體也不可能保持平衡。這種與力大小無關而與最大靜摩擦角有關的平衡條件稱為自鎖條件。物體在這種條件下的平衡現象稱之自鎖現象。
動態受力平衡的分析
動態平衡問題中，光滑平面上物體受三力而平衡，我們通常運用三角形定則，採用繪製重力（方向、大小一定）、支持力（方向一定）、外加力三個力的矢量三角形，的方法，進行研究，解決一些諸如求外力大小的極值、已知外力角度求外力大小等問題。而在粗糙平面上，物體還收到一個摩擦力，對於四力平衡無法繼續使用力的矢量三角形法。這時如果適當運用全反力的知識，便可以將四力轉化成重力（方向、大小一定）、全反力（方向一定）、外加力三力平衡來解決。
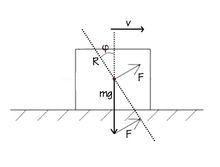利用全反力進行受力分析例：質量為m、電量為+q的物塊置於動摩擦因數為μ的水平面上，加一電場使其恰能向右做勻速直線運動，求所加電場場強的最小值及此時的方向。
如圖，物塊向右勻速運動時，所受電場力F=qE，全反力R與豎直方向夾角φ=arctanμ。由幾何關係（垂線段最短）可知，當F⊥R時F的大小最小，此時E=F/q=mgsinφ/q=mgμ/[q√(μ^2+1)]，方向與水平方向夾角θ=φ=arctanμ。
若不採用全反力模型，也可以將四力分解到水平、豎直兩個方向上分別列出平衡方程，再依據方程組求出F關於θ的函式，利用三角函式的性質求最值。該方法較繁瑣，在此不作贅述。
