![內耗[物理術語]](/img/f/c5e/gZpdmLz91N0cDOzkTM3MTM4ATOxEDMwADMwADMwADMwATMw8yMx8yN08SbvNmLn52bk92bo5Cd0FmLwE2LvoDc0RHa.jpg "內耗[物理術語]")
簡介
葛氏扭擺一個振動物體即使與外界完全隔絕，其振動也會自行減弱，這種現象是由於物體內部微觀結構的“摩擦”，簡稱內耗（內摩擦），消耗了振動系統的彈性儲能。由於應變滯後於應力一個位相角，應力循環一周,應力-應變曲線不能沿原路回到原點，而是形成一個回線，其面積正比於一周的能量消耗，內耗（Q-1）定義為單位體積內每周能量耗損(△W)與最大彈性儲能(W)之比，即 Q-1=△W/W=2πtgφ式中φ 為描述應變(ε)落後於應力（σ）的相差角。Q-1越大，消耗能量越多，對振動的阻尼越大。因此，內耗也可看作材料的阻尼本領。
測量方法
內耗①自由振動衰減法。測量兩個振幅的對數減縮，則一種主要的測量裝置是中國物理學家葛庭燧1947年發明的扭擺,文獻上稱為葛氏扭擺(見彩圖)。其原理如圖1所示:一根絲狀試樣置於加熱爐中懸掛起來,一端固定,另一端被激發振動；當激發停止後,測量扭轉振動振幅的衰減，可以得到內耗作為溫度、頻率或振幅等物理量的函式。近年來已建立了計算機控制的全自動真空倒扭擺。②強迫共振法。測量一棒狀試樣共振頻率（ ωr）、共振峰寬( ω2－ ω1),則內耗為 Q-1=(ω2－ω1)/ωr。③超聲行波衰減法。測量高頻 (106～109Hz)超聲脈衝在試樣中傳播的衰減係數α,測量α作為溫度、頻率、磁場或範性形變等物理量的函式。可計算內耗，其中是超音波在試樣中的波長。
內耗
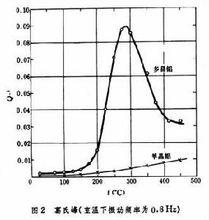
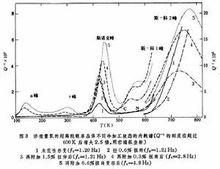
阻片內耗儀內耗峰 對於常見的滯彈性內耗有（見彈性和滯彈性）,掦是引起滯彈性的微觀過程的平均弛豫時間。當 ω掦=1時內耗為極大值。若固定頻率不變，測量內耗隨溫度的變化出現峰值，稱為內耗峰。不同的微觀過程具有不同的特徵弛豫時間，因而使內耗峰出現的溫度不同，形成內耗譜，稱為固體機械能譜。迄今已發現的比較重要的峰如下:①斯諾克（Snoek）峰。體心立方金屬中填隙溶質原子在外應力作用下的擇優取向運動引起的。②曾訥（C.Zener）峰。面心立方金屬中代位溶質原子對（或簇）的應力感生有序引起的。③葛氏峰。金屬晶粒間界的粘滯滑動引起的，早期也稱為晶粒間界峰，它是中國物理學家葛庭燧1947年首先發現的。曲線如圖2所示，從對比的單晶鋁不出現峰值，可見存在於多晶鋁中的晶粒間界內耗峰。根據這個內耗現象，他提出了一種金屬晶界結構模型,現在被稱為葛氏晶界模型。④玻童尼(Bordoni)峰。面心立方金屬冷加工以後低溫下出現的一個與位錯運動有關的峰(見晶體缺陷)。⑤斯－科(Snoek-K?ster)峰。體心立方金屬中位錯與填隙溶質原子互動作用引起的峰，又稱冷加工峰，有人稱為斯-科-葛峰。最近，中國、聯邦德國兩國科學家合作深入研究了這種內耗的機理。在摻氧的超高純鈮單晶體中測得的內耗譜見圖3。
在高分子聚合物中也有α、β、γ等多種峰,分別與高分子的主鏈、側鏈的運動有關。
金屬、非金屬及高分子聚合物中還有許多內耗峰，不一一列舉。
液態內耗儀內耗的理論意義和套用 內耗對材料微觀結構極為敏感，它與金屬中溶質原子微擴散、晶界粘滯性和位錯運動等直接有關,因此,內耗與超聲衰減被廣泛用於研究晶體缺陷、界面、金屬中的擴散、固態相變、超導、疲勞、輻照損傷、薄膜結構等。
例如，研究低溫下金屬和合金的擴散，精確判定擴散常數 D0和擴散激活能 Qi。根據填隙原子引起的內耗峰值和固溶體中的填隙原子濃度成正比，而與沉澱析出的第二相無關，用內耗法測定任一溫度下間隙固溶體的濃度，可確定某些溶解度曲線；或研究應變時效或沉澱析出過程等。還可用於研究固體聲子與聲子、電子以及磁場的互動作用和高分子聚合物的分子結構。工業上用於鋼鐵性能檢驗和阻尼本領測量等。近20年來，內耗與超聲衰減已形成為材料科學、物理冶金和固體物理的一個重要分支學科。
